一、Data Structures (50%)
1. (20%)
Given a red-black tree in the following figure.
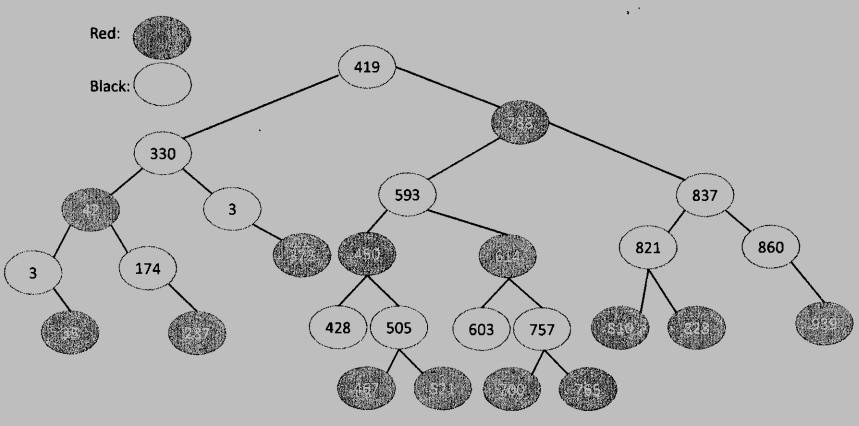
After one node with value 778 is inserted, the resulting red-black tree is shown as follows.
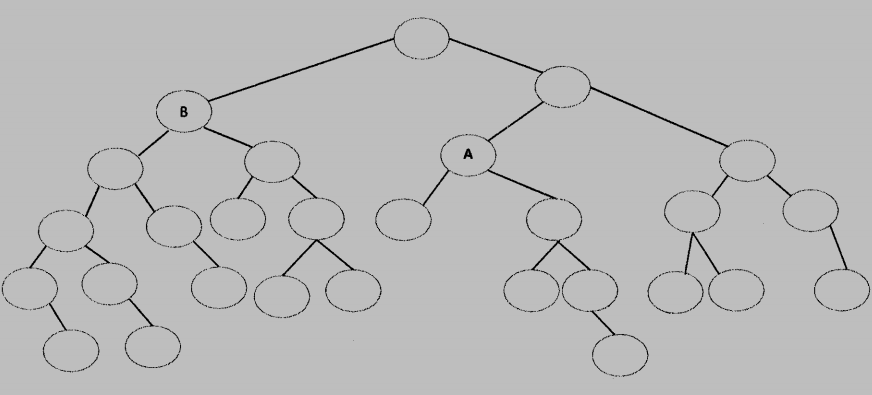
(a) Please describe the operation procedures for this insertion.
(b) Please indicate the color and value of node A and node B, respectively.
參考解答:
(a) 略
(b) node A: black, 614. node B: red, 419.
2. (10%) Given the expression, (x+y)*w+u/(v+x*w)+z, Please show the content in the stack after the operand v is read in postfix transformation.
參考解答:

3. (20%)
(a) Please finish the lost code for the choose function in the following Dijkstra shortest path implementation for a graph without negative-weight edges.
$$程式碼請看原檔$$
(b) In a directed graph without a cycle of negative length but with a negative-length edge, we can implement Bellman-Ford algorithm as follows to compute shortest paths. Please fill in the lost code.
$$程式碼請看原檔$$
參考解答:
(a)
for (i = 0; i < n; i++)
{
if (distance[i] < min && !found[i])
{
min = distance[i];
minpos = i;
}
}(b)
for (int i = 0; i < n; i++)
for (int u = 0; u < n; u++)二、Algorithms (50%)
1. (10%) Prove or disprove: The single-source shortest paths problem can be solved in linear time in directed acyclic graphs.
參考解答:
(1) 找Topological sort.
(2) 從sort的順序由前到後作Bellman-Ford algorithm的Relax function.
2. (15%) The matrix-chain multiplication problem can be stated as follows: Given a chain $(A_1, \, A_2,…, \, A_n)$ of $n$ matrices, where for $i = 1, \, 2,…, \, n,$ matrix $A_i$ has dimension $p_{i-1} \times p_i,$ fully parenthesize the product $A_1A_2…A_n$ in a way that minimizes the number of scalar multiplications. Suppose that you have 6 matrices: $A_1$ has dimension $30 \times 35, \, A_2$ has dimension $35 \times 15, A_3$ has dimension $15 \times 5, \, A_4$ has dimension $5 \times 10, \, A_5$ has dimension $10 \times 20, \, A_6$ has dimension $20 \times 30.$ Please calculate the minimum number of scalar multiplications.
參考解答:16375
3. (10%) Give asymptotic upper and lower bounds for $T(n) = 2T(\dfrac{n}{4}) + \sqrt{n}.$ Assume that $T(n)$ is constant for $n \leq 2.$ Make your bounds as tight as possible.
參考解答:$\Theta (\sqrt{n} lg n)$
4. (15%) Consider the problem of finding the 5-vector $x = (x_i)$ that satisfies
$$
\begin{pmatrix}
1 & -1 & 0 & 0 & 0\\
1 & 0 & 0 & 0 & -1\\
0 & 1 & 0 & 0 & -1\\
-1 & 0 & 1 & 0 & 0\\
-1 & 0 & 0 & 1 & 0\\
0 & 0 & -1 & 1 & 0\\
0 & 0 & -1 & 0 & 1\\
0 & 0 & 0 & -1 & 1\\
\end{pmatrix}
\begin{pmatrix}
x_1\\
x_2\\
x_3\\
x_4\\
x_5
\end{pmatrix}
\leq
\begin{pmatrix}
0\\
-1\\
1\\
5\\
-4\\
-1\\
-3\\
-3
\end{pmatrix}
$$
Determine whether there exists a solution or there is no solution.
參考解答:有負cycle, there is no solution.
試題(pdf):連結
有任何問題,或想要完整解釋的,歡迎在下方留言唷!





發佈留言