102清大資工計科[參考解答]

1. (17%) Answer the following questions.

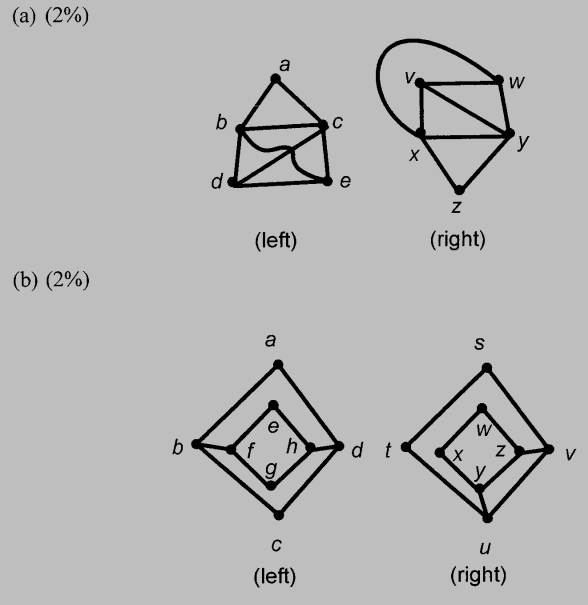
(A) (4%) Prove or disprove whether the two graphs in each subproblem are isomorphic. No point will be given without a formal proof.

(B) (4%) Prove that if $n \in Z^+$ and $n \geq 3,$ then $\prod_{i=2}^n (1 – i^{-2}) = \dfrac{n + 1}{2n}.$
(C) (4%) How many $n < 801, n \in Z^+$ are not divisible by 2, 3, 4, 5, 6, 8, and 10?
(D) (5%) Define $p(x),q(x),$ and $r(x)$ as follows:
$p(x): x^2 – 26x + 120 = 0 \\ q(x): x \text{ is even} \\ r(x): x < 0$
Determine the truth or falsity of the following statements, for the universe of integers. For a false statement, give a counter example.
(a) $\forall x [q(x) \to p(x)]$
(b) $\exists x [q(x) \to p(x)]$
(c) $\exists x [p(x) \to (q(x) \land r(x))]$
(d) $\forall x [\neg q(x) \to \neg p(x)]$
(e) $\forall x [(p(x) \lor q(x)) \to r(x)]$

參考解答：
(A) (a) Two graphs are isomorphic (b) Two graphs are not isomorphic
(B)
$(1 – \dfrac{1}{2^2})(1 – \dfrac{1}{3^2})…(1 – \dfrac{1}{n^2}) = \dfrac{(2 + 1)(2 – 1)}{2^2} \dfrac{(3 + 1)(3 – 1)}{3^2} … \dfrac{(n + 1)(n – 1)}{n^2} = \dfrac{[3 \cdot 4 \cdots (n + 1)][1 \cdot 2 \cdots (n – 1)]}{(2 \cdot 3 \cdots n)^2} = \dfrac{(n + 1)!(n – 1)!}{2(n!)(n!)} = \dfrac{n + 1}{2n}$
(C) 214
(D) (a) F (b) T (c) T (d) T (e) F

---

2. (17%) Answer the following questions.

(A) (5%) Solve the following recurrence:
$$G_0 = 1, \, G_1 = 2, \, G_k = 5G_{k-1} + 6G_{k-2} \text{ for } k \geq 2.$$
(B) (4%) In a 10-sided polygon,
(i) How many diagonals are there?
(ii) Suppose that no three diagonals meet at one point. How many intersections will the diagonals form?
(C) (4%) How many positive integer solutions (x, y, z) for the following inequality?
$$x + y + z \leq 100$$
(D) (4%) Find the greatest common divisor of 41537 and 248419.

參考解答：
(A) $G_k = \dfrac{1}{7} [4 \times (-1)^k + 3 \times 6^k], \text{ for } k \geq 0.$
(B) (i) 35 (ii) $\binom{10}{4}$
(C) 161700
(D) 73

---

3. (17%) Answer the following questions.

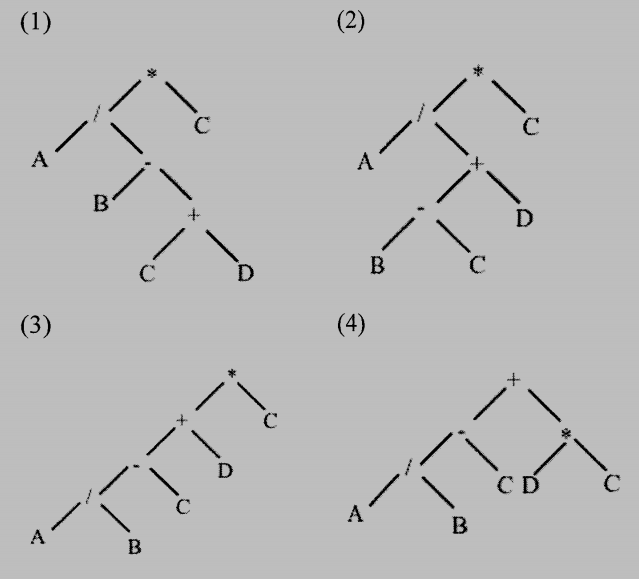
(A) Consider the infix expression (A/(B-C+D))*C and answer the following two questions:
(a) (3%) Which of the following is the expression tree of the given expression?

(b) (4%) Write down the equivalent postfix expression.
(B) Consider using arrays as the underlying representations of binary trees. Answer the following questions.
(a) (4%) Insert a set of keys 8, 29, 14, 16, 31, 19, 13 in this order into an initially empty max heap H. Show the content of the array that stores H.
(b) (3%) Insert a set of keys 27, 3, 15, 2, 30 into an initially empty binary search tree T. Show the content of the array that stores T.
(c) (3%) Treat H as a priority queue, pop two keys from it, and then insert the two keys into T. Show the content of the array that stores T again.

參考解答：
(A) (a) 2 (b) ABC-D+/C*
(B)
(a)

Index	0	1	2	3	4	5	6
Value	31	29	19	8	16	14	13

(b)

Index	0	1	2	3	4
Value	27	3	30	2	15

(c)

Index	0	1	2	3	4	5	6
Value	27	3	30	2	15	29	31

---

4. (17%) Answer the following questions.

(A) (2%) Please choose an answer that best completes the following sentence: The number of comparisons required to find an element in a hash table with $N$ buckets, of which $M$ are full,
(a) is approximately $log_2M.$
(b) is approximately $log_2N.$
(c) is usually only slightly less than $N.$
(d) may be large if $M$ is only slightly less than $N.$
(B) (9%)
(a) How many different binary trees can be made from three nodes that contain the key values 1, 2, and 3? Explain why.
(b) How many different binary search trees can be made from three nodes that contain the key values 1, 2, and 3? Explain why.
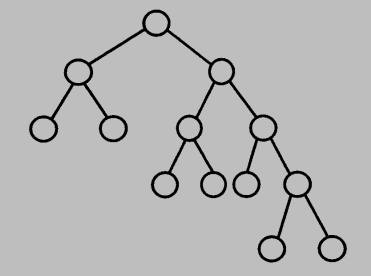
(c) Color the nodes in the following tree so that it is a red-black tree.

(C) (6%)
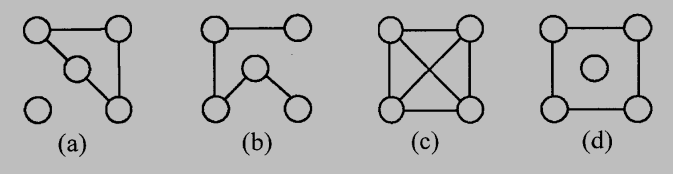
(a) Which of the following graphs are bipartite?
(b) Which of the following graphs are biconnected?
(c) What are the real-world applications that would use the biconnected graph? Please give an example.

參考解答：
(A) D
(B) (a) 30 (b) 5
(c)

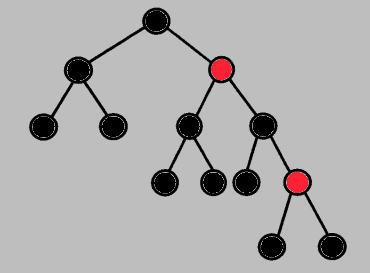
(C) (a) a, b, d (b) c (c) Network services would use the biconnected graph. When building a network, we don’t want the entire system to shut down with only one node failure.

---

5. (17%) Answer the following questions.

(A) (9%) Consider the following C program of a recursive function:

void f(int n)
{
    int i;
    
    if (n > 1) {
        for (i = 1; i <= n; i++) {
            printf("Computer Science.\n");
        }
        f(n/2);
        f(n/2);
    }
}

(a) How many lines does the program print if we call f(1024)?
(b) Write a recurrence relation for the time complexity.
(c) How many lines, as a function of n in $\Theta (\cdot)$ form, does the program print? Assume n is a power of 2.
(B) (6%) The following code block is an implementation of Floyd’s algorithm for finding all-pairs shortest paths. Initially, dist[i][j] is the length of the directed edge from vertex i and vertex j if it exists, and is infinity otherwise. Please write down the missing code for (a) and (b).

for (k = 1; k <= N; k++)
    for (i = 1; i <= N; i++)
        for (j = 1; j <= N; j++)
            dist[i][j] = min((a), (b));

(C) (2%) Please describe the maximum-flow problem.

參考解答：
(A) (a) 10240 (b) $T(n) = 2T(\dfrac{n}{2}) + O(n)$ (c) $\Theta (nlogn)$
(B) (a) dist[i][j] (b) dist[i][k] + dist[k][j]
(C) Given a graph with its capacity of every edges. We need to find the maximum flow from the source to the sink.

---

6. (15%) Answer the following questions.

(A) (10%) Let A(1:n,1:n) be a positive definite matrix. The following algorithm takes a positive definite matrix A, as input and decomposes A into the product of L and $L^t$ (the transpose of matrix L), where L is a lower triangular matrix stored in the diagonal and lower part of A.

for j = 1,2,...,n
{
    t = A(j,j);
    
    for r = 1,2,...,j-1
    { t = t - A(j,r) * A(j,r); }
    
    A(j,j) = sqrt(t);
    
    for i = j+1,j+2,...,n
    {
        s = A(i,j);
        
        for r = 1,2,...,j-1
        { s = s - A(i,r) * A(j,r); }
        
        A(i,j) = s / A(j,j);
    }
}

Give the following matrix A(1:3,1:3) as input
$
A =
\begin{bmatrix}
9 & 3 & -3\\
3 & 17 & 3\\
-3 & 3 & 27
\end{bmatrix}
$
What is the result of A after running the algorithm? (Show only the integer part)
(B) (5%) Let a and n be positive integers with $1 < a < n$ and gcd(a,n) = 1, that is, they are relatively prime. The order of $a \, mod \, n$ is the smallest positive integer r such that $a^r \equiv 1 (mod \, n),$ we denote $r = ord_n(a).$ For example, $ord_4(3) = 2.$
(a) What is $ord_{11}(3)?$
(b) What is $ord_{31}(3)?$

參考解答：
(A)
$
\begin{bmatrix}
3 & 1 & -1\\
1 & 4 & 1\\
-1 & 1 & 5
\end{bmatrix}
$
(B) (a) 5 (b) 30

---

試題(pdf)：連結

有任何問題，或想要完整解釋的，歡迎在下方留言唷！