1. (10%)

Complete the above C program to produce the permutations of 1, 2, 3 in the following order: 231, 321, 312, 132, 213, 123.
參考解答:
(a) temp = *x;
(b) *x = *y;
(c) *y = temp;
(d) start == end
(e) “%s”, start
(f) cp = start
(g) cp <= end
(h) cp, end
(i) start, end-1
(j) cp, end
2. (6%) Consider a modification to merge sort in which $n/k$ sub-lists of length $k$ are sorted using quicksort and then merged using the standard merging mechanism, where $n$ is the input size and $k \leq n$ is a given integer. Answer the following two questions in terms of $n$ and $k.$
(a) What is the worst-case time complexity of the above modified merge sort?
(b) What is the average-case time complexity of the above modified merge sort?
參考解答:(a) $O(nk)$ (b) $O(nlgk)$
3. (7%) A sequence of left and right parentheses is well-formed if the parentheses are properly nested. Give an efficient algorithm to determine whether a given sequence $S$ of left and right parentheses is well-formed. Use $S = “((())())”$ as an example to explain your algorithm. Let $|S| = n.$ What is the time complexity of your algorithm in terms of $n?$
參考解答:$O(n)$
4. (7%) Let $A$ be an array that stores $n$ integers in $[1, 2^{loglogn \times logn}].$ Give an efficient algorithm to sort the integers in $A.$ The time complexity of your algorithm must be better than $O(nlogn).$ What is the time complexity of your algorithm in terms of $n?$
參考解答:略
5.
(a) (2%) Suppose the frequencies of the characters A, B, C, D, E, and F are 26, 9, 17, 11, 23, 14, respectively. Construct a Huffman tree for these characters.
(b) (5%) In general, let $f_1,f_2,…,f_n$ denote the frequencies of $n$ characters. Give an $O(nlogn)$-time algorithm to construct a Huffman tree for these $n$ characters.
參考解答:
(a)
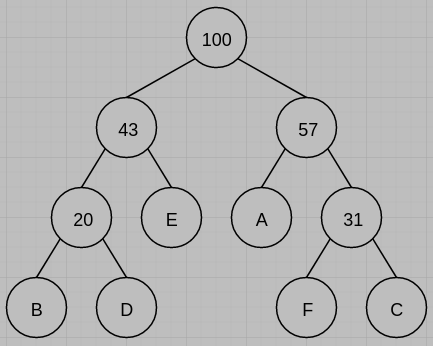
(b) 先花 $O(nlogn)$ 的時間把 $n$ 比資料的frequencies排序好,再用greedy algorithm的方式慢慢建Huffman tree.
6. (6%) Suppose we have $n$ ranges $[a_1,b_1],[a_2,b_2],…,[a_n,b_n],$ where all $a_i$’s are negative, and all $b_i$’s are positive. We are asked to preprocess these ranges so that for any input value $x,$ we can efficiently count the number of ranges containing $x.$ Design an efficient representation of the ranges so that the desired counting can be done in $O(logn)$ time. Your representation must take $O(n)$ space. Describe your representation and how to answer a query in $O(logn)$ time in details.
參考解答:
X = sorted list based on a
Y = sorted list based on b
if x == 0:
return n;
if x > 0:
Binary Search in Y;
return (n - index);
if x < 0:
Binary Search in X;
return index;7. (7%) Consider a queue with $n$ elements. We define the middle element of the queue to be its $\lceil n/2 \rceil$th element, counting from the front. For example, suppose the queue contains the elements A, B, C from front to end, then the middle element is B. If the queue contains the elements D, E, F, G from front to end, then the middle element is E. Note that when we perform the usual ENQUEUE or DEQUEUE operation, the middle element may change. Suppose we want to implement a special queue that supports, apart from the usual ENQUEUE and DEQUEUE, the following operation:
EXTRACT_MID: Remove the middle element from the queue.
For example, after EXTRACT_MID in the above queue with D, E, F, G, the element E is extracted and the queue will contain D, F, G from front to end. Give an efficient implementation of the above special queue, so that each operation ENQUEUE, DEQUEUE, and EXTRACT_MID can be performed in $O(1)$ time.
參考解答:多一個middle_pointer指向MID前一個element, 並且改用double linked list.
8. (6%) Among 150 students, 70 students are wearing hats, 60 are wearing gloves, and 37 are wearing both hats and gloves. Of the 65 students who are wearing sweaters, 32 are wearing hats, 28 are wearing gloves, and 17 are wearing both hats and gloves. Everyone wearing neither a hat nor gloves is wearing scarves.
(a) How many students are wearing scarves?
(b) How many students not wearing a sweater are wearing hats but not gloves?
(c) How many students not wearing a sweater are wearing neither a hat nor gloves?
參考解答:(a) 57 (b) 18 (c) 35
9. (6%) Consider the equation $x_1 + x_2 + x_3 + x_4 = 13.$
(a) How many different integer solutions to the equation in which $x_i \geq 1, i = 1, 2, 3, 4?$ (Note that the two solutions $x_1 = 5, x_2 = 4, x_3 = 3, x_4 = 1 \text{ and } x_1 = 1, x_2 = 4, x_3 = 5, x_4 = 3$ are assumed to be different.)
(b) How many distinct integer solutions in which $1 \leq x_i \leq 4, i = 1, 2, 3, 4?$
參考解答:
(a) $\binom{12}{3}$
(b) $\binom{4}{0}\binom{12}{9} – \binom{4}{1}\binom{8}{5} + \binom{4}{2}\binom{4}{1}$
10. (7%) Given the set $A = \{1, 2, 3, 4, 6, 12\},$ consider the partial ordering relation $R$ on $A.$
$$R = \{(x,y) | x \text{ divides } y\}.$$
(a) Draw the Hasse diagram for the partially ordered set $(A, R).$
(b) What is the length of the longest chain in the partially ordered set $(A, R)?$ Suppose the length of the longest chains in $(A, R)$ is $n,$ then the elements in $A$ can be partitioned into $n$ disjount antichains. Please find one such partition.
參考解答:
(a)
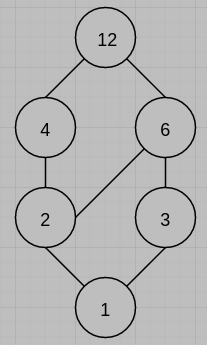
(b) $\{1,2,4,12\}$ is a 4-length chain, $\{\{1\},\{2,3\},\{4,6\},\{12\}\}$ is a disjoint antichains.
11. (6%) In a graph $G,$ a set $I \subseteq V(G)$ is an independent set if vertices in $I$ are pairwise nonadjacent, and a set $D \subseteq V(G)$ is a dominating set if every vertex not in $D$ has a neighbor in $D.$ Show that for any graph, the minimum size of a dominating set is not greater than the maximum size of an independent set.
參考解答:略
12. (6%) In a type-2 grammer, every production is of the form $A \to \alpha,$ where $A$ is a single non-terminal, and $\alpha$ is a string consisting of terminals and non-terminals. Please find a type-2 grammer for $L = \{a^nb^mc^k:k = |n – m|\}.$
參考解答:略
13. (7%) How many nonidentical (though some may be isomorphic) spanning trees are there for the following subgraphs of $G$ (shown in Fig. 1)?
(a) $G_1:$ the subgraph of $G$ induced by the vertices $a,b,c,$ and $d.$
(b) $G_2:$ the subgraph of $G$ obtained by removing edge $(c,h)$ from $G.$
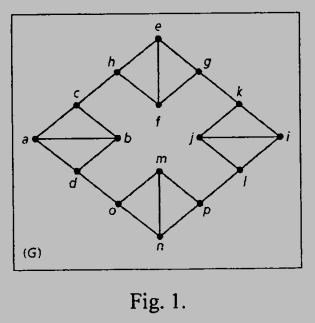
參考解答:(a) $8$ (b) $8^4$
14. (6%) Let $a_r$ denote the number of ways of selecting $r$ objects from $n$ objects with unlimited repetitions.
(a) Since each object can be selected as many times as we wish, $a_r$ is equal to the coefficient of $z^r$ in _____.
(b) The contribution from each of the above factors will correspond to the number of times one of the object is selected. Prove that $a_r = C(n+r-1,r).$
參考解答:
(a) $(\dfrac{1}{1 – z})^n$
(b) 略
15. (6%) There are two kinds of particles inside a nuclear reactor. In every second, an $\alpha$ particle will split into three $\beta$ particles, and a $\beta$ particle will split into an $\alpha$ particle and two $\beta$ particles. If there is a single $\alpha$ particle in the reactor at $t = 0,$ how many particles are there altogether at $t = 100.$
參考解答:$3^{100}$
試題(pdf):連結
有任何問題,或想要完整解釋的,歡迎在下方留言唷!





jcchen
12.分為兩種處理,參考
https://stackoverflow.com/questions/50244001/context-free-grammar-where-of-one-terminal-equals-difference-of-other-two
mt
感謝提供資料~