1. (5%) A two dimensional array D with X rows and Y columns is stored in memory in row-major order. Each element of array D occupies B memory locations. The element at the first row and first column is D[1][1]. Let the address of the first memory location of D[1][1] be S. Find the address of the first memory location of D[i][j].
參考解答:$S + [Y(i-1) + (j-1)]B$
2. (12%) A circular queue can be implemented using an array. Two integer variables, namely, start and end, can be used to keep track of the first element and the last element of the queue.
(a) Without using any additional variable, how can a full queue be distinguished from an empty queue?
(b) How can a full queue be distinguished from an empty queue by using one additional bit?
參考解答:
Assume array has n entries
(a)
if (start == end) return empty;
if ((end + 1)%n == start) return full;
(b)
if (start == end && !full) return empty;
if (start == end && full) return full;3. (5%) For each statement below, state if it is true or false.
(a) For any tree, each internal node has two child nodes.
(b) The number of edges is one more than the number of nodes in a tree.
(c) The hight of any binary tree is at most $log_2n+1$ where $n$ is the number of nodes.
(d) A tree can have at most one cycle.
(e) There is a unique path between every two nodes in a tree.
參考解答:(a) F (b) F (c) F (d) F (e) T
4. (6%) Let $p$ and $q$ be two propositions. Given that the value of $p \to q$ is false, determine the value of $(\sim p \lor \sim q) \to (\sim q)$ with a brief explanation.
參考解答:True
5. (6%) Let $n_k$ be the number of k-bit binary numbers that have no three consecutive 0s. Derive a recurrence relation for $n_k.$ (Don’t forget to write down the base case(s).)
參考解答:$n_k = n_{k-1} + n_{k-2} + n_{k-3}, \forall n \geq 4. \ n_1 = 2, n_2 = 4, n_3 = 7.$
6. (8%) Rank the following functions by order of growth; that is, give an ordered list of the functions $g_1,g_2,…,g_8$ satisfying $g_1 = \Omega(g_2), g_2 = \Omega(g_3),$ and so on. Partition your list into equivalence classes using brackets, e.g., $[g_1,g_2],[g_3,…,g_8],$ such that $g_i$ and $g_j$ are in the same class if and only if $g_i = \Theta(g_j).$
$$n^2, (lgn)!, (3/2)^n, lg(n!), (lgn)^{lgn}, (n+1)!, nlgn, 4^{lgn}$$
參考解答:$(n+1)!, (3/2)^n, (lgn)^{lgn}, (lgn)!, [n^2, 4^{lgn}], [nlgn, lg(n!)]$
7. (6%) Let $B_n$ denote the number of binary trees of $n$ nodes and let $H_n$ denote the number of different binary trees of height $h.$ Write down the recurrence equations of $B_n$ and $H_n$ respectively.
參考解答:$B_n = B_0B_{n-1} + B_1B_{n-2} +…+ B_{n-1}B_0, B_0 = B_1 = 1. \\ H_n = H_{n-1}H_{n-1} + 2H_{n-1}(H_0 + H_1 +…+ H_{n-2}), H_0 = 1, H_1 = 3.$
8. (3%) Define the fractional knapsack problem as follows. Suppose there are $n$ items in a store, each with weight $w_i > 0$ and value $v_i > 0, i = 1,2,…,n.$ Our target is to determine the fraction $x_i, 0 < x_i < 1,$ for each item $i,$ such that these fractions of items can be put into a knapsack carrying weight $W$ (that is, $\sum_{i=1}^n x_iw_i \leq W$), and the total value $\sum_{i=1}^n x_iv_i$ is maximized. Describe an algorithm with the worst-case time complexity $O(nlogn)$ that solves the fractional knapsack problem.
參考解答:
(1) Sort values per weight unit.
(2) Start by choosing items with highest value/weight until the bag is full (greedy).
9. (8%) In the following max-heap tree, please perform the DeleteMaximum operations twice and show the intermediate steps (whenever some data moves).
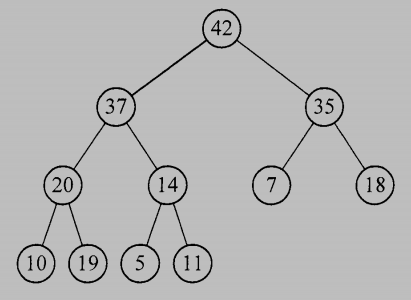
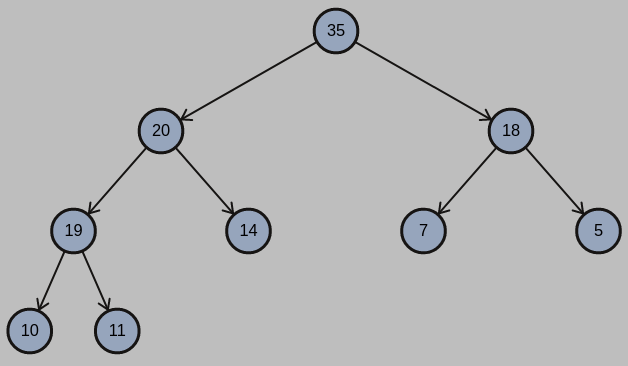
參考解答:
10. (9%) Consider the following connected weighted graph $G.$
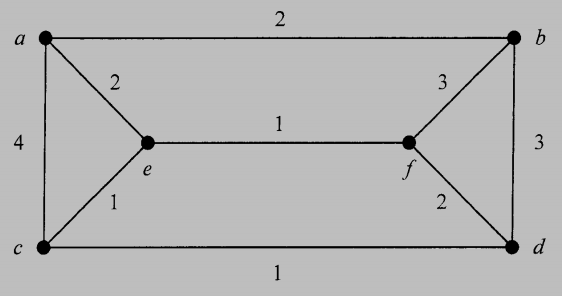
Please run Dijkstra’s algorithm on graph $G$ with starting vertex $a.$ Please show the intermediate steps and highlight the shortest path tree edges in each step.
參考解答:
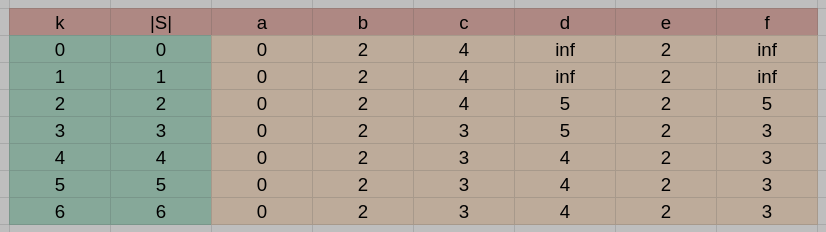
11. (8%) Of the 2300 delegates at a political convention, 1542 voted in favor of a motion to decrease the deflict, 569 voted in favor of a motion dealing with environmental issues, and 1197 voted in favor of a motion not to increase taxes. Of those voting in favor of the motion concerning environmental issues, 327 also voted to decrease the deflict, and 92 voted not to increase taxes. Eight hundred and thirty-nine people voted to decrease the deflict while also voting against increasing taxes but, of these 839, only 50 voted also in favor of the motion dealing with the environment.
(a) How many delegates did not vote in favor of any of the three motions?
(b) How many of those who voted against increasing taxes voted in favor of neither of the other two motions?
參考解答:(a) 200 (b) 316
12. (8%) A connected, planar graph has nine vertices having degrees 2, 2, 2, 3, 3, 3, 4, 4, and 5.
(a) How many edges are there?
(b) How many faces are there?
參考解答:(a) 14 (b) 7
13.
(a) (4%) Let $X = \{1,2,…,n\}.$ For a subset of $X,$ we say that it covers its elements. Given a set $S = \{S_1,S_2,…,S_m\}$ of $m$ subsets of $X$ such that $\bigcup_{i=1}^m S_i = X,$ the set cover problem is to find the smallest subset $T$ of $S$ whose union is equal to $X,$ that is, $\bigcup_{S_i \in T} S_i = X.$ For example, suppose that $X = \{1,2,…,5\}$ and there are the following four subsets in $S: S_1 = \{1,3,4\}, S_2 = \{2,5\}, S_3 = \{1,5\}$ and $S_4 = \{2,4\}.$ Then the optimal set cover is $\{S_1,S_2\}.$ Please give a counterexample for the following greedy algorithm: At each stage, the algorithm picks the set that covers the greatest number of remaining elements that are uncovered. Please also write down the greedy and optimal solutions of your counterexample.
(b) (6%) Suppose that each subset $S_i$ in $S$ contains only two elements. Can the set cover problem then be solved in polynomial time? If yes, please also design a polynomial-time algorithm to solve this set cover problem and analyze its time complexity. If no, please also describe your reason.
參考解答:
(a)
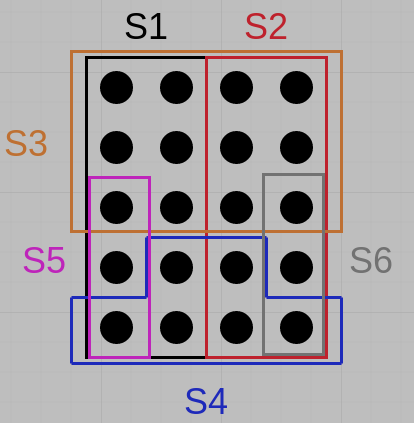
Answer found by this greedy algorithm is $S_3,S_4,S_5,S_6,$ but the answer is $S_1,S_2.$
(b) 略
14. (6%) Given positive integers $C > 1$ and $n,$ the n-tuple optimization problem is to determine whether there exist positive integers $c_1,c_2,…,c_n$ such that $\prod_{i=1}^n c_i = C$ and $\sum_{i=1}^n c_i$ is minimized. The prime number problem is to determine whether a given positive integer is a prime number or not. Please prove that if the n-tuple optimization problem can be solved in polynomial time, then the prime number problem can be solved in polynomial time.
參考解答:略
試題(pdf):連結
有任何問題,或想要完整解釋的,歡迎在下方留言唷!





發佈留言