102成大資工程設[參考解答]

Data Structure (50%)

一、是非題 (15%)

1. Let T be a minimum spanning tree of G. Then, for any pair of vertices s and t, the shortest path from s to t in G is the path from s to t in T.

參考解答：F

---

2. The function $\lceil lgn \rceil !$ is polynomially bounded.

參考解答：F

---

3. If the depth-first search of a graph G yields no back edges, then the graph G is acyclic.

參考解答：T

---

4. Suppose P1 and P2 are problems and P1 $\leq _p$ P2. If P2 can be solved by an algorithm with time complexity $\lceil lglgn \rceil !,$ then P1 $\in P.$

參考解答：T

---

5. Sorting 8 elements with a comparison sort requires 24 comparisons in the worst case.

參考解答：F

---

二、計算題 (25%)

1. (10%) Use the recursion-tree method to solve the recurrence $T(n) = 2T(n/2) + n/lgn.$

參考解答：$\Theta (nlglgn)$

---

2. (10%) For COIN-CHANGE problem defined below, please calculate (a) how many different subproblems overall and (b) how many choices we have in determining which subproblem(s) to use in an optimal solution. [COIN-CHANGE Problem: An amount of money $M,$ and an array of $d$ denominations $c = (c_1, \, c_2,…,c_d),$ in a decreasing order of value $(c_1 > c_2 > … > c_4).$ Please find a list of $d$ integers $i_1, \, i_2,…, \, i_d$ such that $c_1 \times i_1 + c_2 \times i_2 + … + c_d \times i_d = M$ and $i_1 + i_2 + … + i_d$ is minimal.]

參考解答：
(a) M
(b) d

---

3. (15%) Please analysis the running time of Dijkstra’s algorithm under the following data structure implementation (1) array, (2) binary heap, and (3) Fibonacci heap [where Extract-Min $O(lgV),$ Decrease-Key $O(1)$]

參考解答：
(1) $O(V^2)$
(2) $O(ElgV + VlgV)$
(3) $O(VlgV + E)$

---

Algorithms (50%)

1. (15%) Consider the following graph:

$$圖片請看原檔$$

Compute minimum cost and construct minimum spanning tree step by step using:
(1) Kruskal’s algorithm
(2) Prim’s algorithm
(3) Sollin’s algorithm

參考解答：
Minimum cost: 64
MST:

---

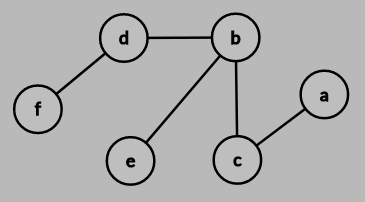
2. (15%) Jeremy is a waiter working in a restaurant. The chef there is sloppy; when he prepares a stack of pancakes, they come out all different sizes. When Jeremy delivers the pancakes to the customer, he wants to rearrange them by grabbing several from the top and flipping them over on the way. After repeating this for several times, the smallest pancake is on top, and so on, down to the largest at the bottom. If there are n pancakes, how many flips are required? Design an algorithm to help Jeremy, and analyze its time complexity.

參考解答：Every time we choose the biggest pancake, and flip once to get that pancake to the top and flip again to put it at the bottom, so it needs 2 flips for every pancakes except the smallest one. It requires $2(n-1)$ flips in total.

---

3. (20%) A Bloom Filter is a space-efficient probabilistic data structure used to test whether a key is in a large data set. Instead of answering “yes” or “no,” a Bloom Filter answers “maybe” or “no.” A Bloom Filter consists of m bits of memory and h uniform and independent hash functions $f_1, \, f_2,…, \, f_h.$ Each $f_i$ hashes a key k to an integer in the range $[1, \, m].$ Initially all m filter bits are zero, and the data set is empty. When key k is added to the data set, bits $f_1(k), \, f_2(k),…, \, f_h(k)$ of the filter are set to 1. When a query “Is key k is in the data set?” is made, bits $f_1(k), \, f_2(k),…, \, f_h(k)$ are examined. The query answer is “maybe” if all these bits are 1. Otherwise, the answer is “no.”

(1) When the answer is “no,” the key is not in the data set; when the answer is “maybe,” the key may or may not be in the data set. Explain why.
(2) A filter error occurs whenever the answer is “maybe” and the key is not in the data set. Assume that key k is an integer in the range $[1, \, n]$ and u updates are made. Compute the probability of filter error for an arbitrary query after the u-th update.

參考解答：
(1) 因為不同key值可能對應到相同的memory bit造成就算k沒被加進data set, 還是有機會造成$f_i(k)$ set成1的case.
(2)
With m bits, h hash function, u updates
proability that a certain bit is still 0 after inserted n elements is $(1 – \dfrac{1}{m})^{hu}$
The proability that a certain bit is 1: $1 – (1 – \dfrac{1}{m})^{hu}$
So the proability of filter error is: $(1 – (1 – \dfrac{1}{m})^{hu})^h$

---

試題(pdf)：連結

有任何問題，或想要完整解釋的，歡迎在下方留言唷！