1. (20%) Don’t just write down the answer without explanations.
(a) Determine the number of paths in the xy-plane from $(m,n)$ to $(p,q),$ $m,n,p,q \in$ positive integer or zero, $m < p, \, n < q,$ where each such path is made up of individual steps going one unit to the right $(x,y) \rightarrow (x+1,y)$ or one unit upward $(x,y) \rightarrow (x,y+1).$
(b) If $(m,n) = (0,0), \, (p,q) = (7,4),$ how many of the paths in part (a) do not use the path from $(2,2)$ to $(3,2)$ to $(4,2)$ to $(4,3)?$
(c) If $(m,n) = (0,0), \, (p,q) = (7,4),$ how many of the paths in part (a) do not pass through the points $(0,1), \, (1,2), \, (2,3), \, (3,4)?$
(d) If an additional type of move $(x,y) \rightarrow (x+1,y+1)$ is allowed, how many of the paths in part (a) if $(m,n) = (0,0), \, (p,q) = (7,4)?$
參考解答:
(a) $\dfrac{(p-m) + (q-n)}{(p-m)!(q-n)!}$
(b) $\binom{11}{7} – \binom{4}{2} \binom{4}{1}$
(c) $\binom{11}{7} – \binom{11}{3}$
(d) $\binom{11}{7} + \dfrac{10!}{6!3!} + \dfrac{9!}{5!2!2!} + \dfrac{8!}{4!1!3!} + \dfrac{7!}{3!4!}$
2. (20%) Don’t just write down the answer without explanations.
(a) If the cost of each edge is given, determine the cost of the minimum spanning tree in the following figure?
$$圖片請看原檔$$
(b) How many different spanning trees in the following figure?
$$圖片請看原檔$$
(c) How many different spanning trees in the following figure?
$$圖片請看原檔$$
參考解答:(a) 29 (b) 40 (c) $4 \times 40^4$
3. (10%) Find a formula for the convolution of each of the following pairs of sequences where n belongs to integers.
(a) $a_n = 1, \, 0 \leq n \leq 5, \, a_n = 0, \, \forall n \geq 6; \\ b_n = n, \, \forall n \geq 1.$
(b) $a_n = (-1)^n, \, b_n = (-1)^n, \, \forall n \geq 1.$
參考解答:
(a)
$c_n = 6n – 15, \, \forall n \geq 6. \\ c_0 = 0, \, c_1 = 1, \, c_2 = 2, \, c_3 = 6, \, c_4 = 10, \, c_5 = 15.$
(b)
$c_0 = c_1 = 0, \, c_n = (n-1)(-1)^n, \, \forall n \geq 2.$
試題(pdf):連結
有任何問題,或想要完整解釋的,歡迎在下方留言唷!





leo
不好意思
想請問2(b)的40是怎麼算的
mt
這題我是用Kirchhoff’s Theorem算的喔~可以參考這部影片。
tinge
請問一下最後一題的a跟b是怎麼算的
mt
可以參考下圖:
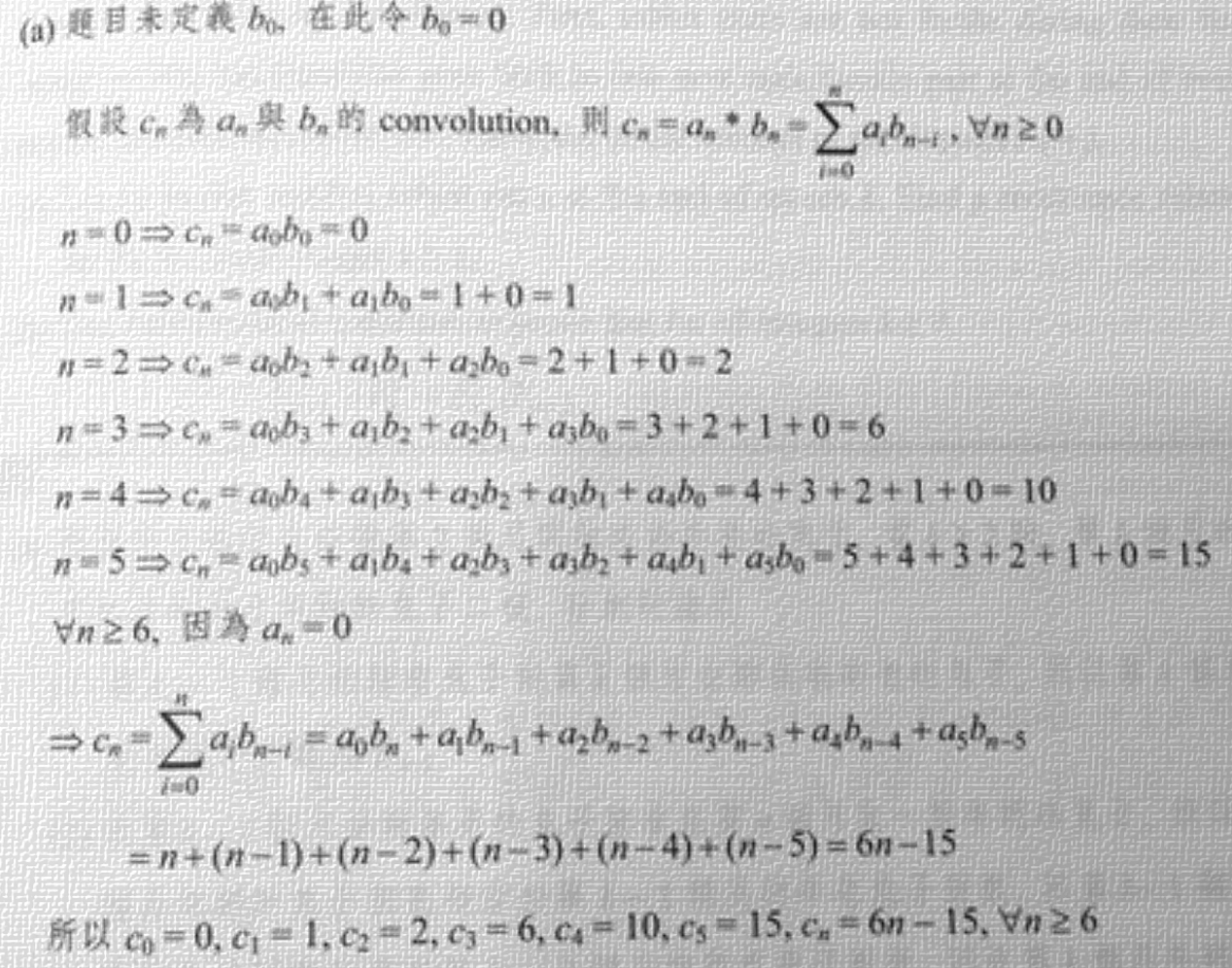
tinge
感謝~
tinge
(答案是不是反了)
mt
已更正!感謝~