104清大資工計科[參考解答]

1. (5%) Among all n-digit numbers, how many of them contain the digits 2 and 7 but not the digits 0, 8, 9?

參考解答：$7^n – 2 \cdot 6^n + 5^n$

---

2. (5%) In how many ways can 2n people be divided into n pairs?

參考解答：$\dfrac{(2n)!}{2^n \cdot n!}$

---

3. (7%) Let R be a transitive and reflexive relation on A. Let T be a relation on A such that (a,b) is in T if and only if both (a,b) and (b,a) are in R. Show that T is an equivalence relation.

參考解答：
Reflexive: Since $\forall a \in A, \, (a,a) \in R$ so $(a,a) \in T$ too.
Symmetric: If $(a,b) \in T,$ that means $(a,b) \in R \land (b,a) \in R,$ so $(b,a) \text{ is also } \in T.$
Transitive: Assume $(a,b) \text{ and } (b,c) \in T,$ then $(a,b),(b,c),(b,a),(c,b) \text{ is also } \in R.$ Since $R$ satisfies transitive, $(a,c) \text{ and } (c,a) \in R,$ so both of them also belongs to T.
Since T satisfies reflexive, symmetric and transitive, so it is an equivalence relation.

---

4. (8%) Given a recursive definition of $a_n: \, a_1 = 1; \, a_{k+1} = 3a_k + 1 \text{ for } k \geq 1,$ please derive a close-form formula for $a_n,$ and then prove that your formula is correct. (Hint: Write down the first six numbers $(a_1,a_2,a_3,a_4,a_5,a_6)$ and guess the formula).

參考解答：$a_n = \dfrac{1}{2} (3^n – 1), \, n \geq 1.$

---

5. (8%) Prove by induction that $3^{2n} – 1$ is divisible by 8 for all $n \geq 1.$

參考解答：
When $n = 1, \, 3^2 – 1 = 8$ is divisible by 8.
Assume when $n = k – 1,$ the hypotesis is correct.
When $n = k, \, 3^{2k} – 1 = (3^{2k-2} – 1) \times 3^2 + 8.$
Since $3^{2k-1} – 1$ is divisible by 8, so it’s obvious that $(3^{2k-2} – 1) \times 3^2 + 8$ is also divisible by 8.
得證。

---

6. (10%) Answer the following questions about binary trees.

(a) Given an initially empty min heap H, draw the min heap after the following operations: insert 34, insert 12, insert 28, delete-min, insert 9, insert 30, insert 15, and insert 5.
(b) Treat H as a priority queue where a key with a smaller value is of higher priority. Draw H after popping three keys out of it.
(c) Insert the three keys popped out from H in question (b) into an initially empty binary tree T, and then insert three other keys 45, 3, and 12. Draw T after completing these operations.

參考解答：
(a)

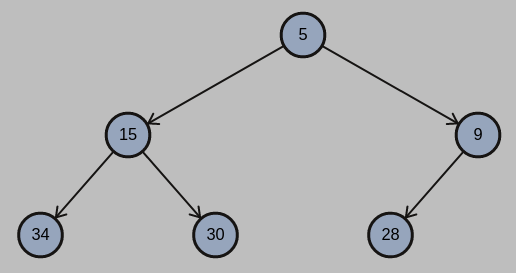
(b)

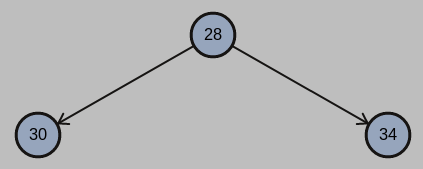
(c)

---

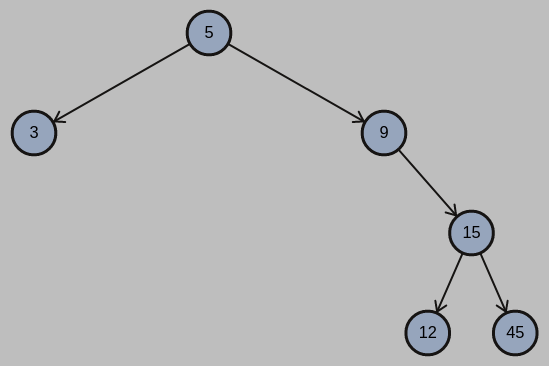
7. (6%) Answer the following questions about triangular matrix.

(a) In a lower triangular matrix, A, with n rows. What’s the total number of nonzero terms?
(b) Since storing a triangular matrix as a two dimensional array wastes space, we would like to find a way to store only the nonzero terms of the triangular matrix in a one dimensional array. Find the index of $A_{i,j}$ in a one dimensional array $b$ if we store $A_{1,1}$ at $b[0].$

參考解答：(a) $\dfrac{n(n+1)}{2}$ (b) $\dfrac{i(i-1)}{2} + j – 1$

---

8. (8%) Consider the following graph G represented by an adjacency list. Assume the dfn[3] = 5 and dfn[4] = 6 after we invoke the function dfnlow (as shown below) with the call dfnlow(5, -1) being executed. Then, after the function dfnlow(5, -1) is invoked,

(a) what is the value of dfn[1]?
(b) what is the value of low[1]?
(c) what is the value of low[2]?

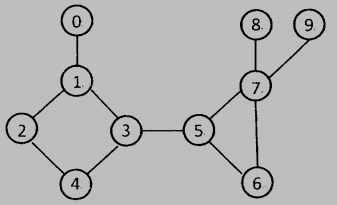
The C declarations for adjacency list representation and function dfnlow():

#define MIN2 (x,y) ((x) < (y) ? (x) : (y))
#define MAX_VERTICES 100

typedef struct node *node_pointer;
typedef struct node {
    int vertex;
    struct node *link;
};
node_pointer graph[MAX_VERTICES];

int dfn[MAX_VERTICES], low[MAX_VERTICES];
int num;

void dfnlow(int u, int v)
{
    /* v is the parent of u (if any). It is assumed that all entries of all dfn[] and low[] have been initialized to -1 and num been initialized to 0. */
    node_pointer ptr;
    int w;
    dfn[u] = low[u] = num++;
    
    for (ptr = graph[u]; ptr; ptr = ptr -> link) {
        w = ptr -> vertex;
        
        if (dfn[w] < 0) { /* w is an unvisited vertex */
            dfnlow(w, u);
            low[u] = MIN2(low[u], low[w]);
        }
        else if (w != v)
            low[u] = MIN2(low[u], dfn[w]); 
    }
}

參考解答：(a) 8 (b) 5 (c) 5

---

9. (9%) In heap sort, function adjust, heapInitialization, and heapSort (as shown below) are used. The function adjust starts with a binary tree whose left and right subtrees are max heaps and rearranges records so that the entire binary tree is a max heap, and the functions heapInitialization and heapSort use a series of adjusts to initialize the heap and perform a heap sort on a[1:n], respectively. Please analyze the complexities of:

(a) adjust.
(b) heapInitialization.
(c) heapSort.

The C declarations for heap and functions adjust(), heapInitialization(), and heapSort():

heapSort():
    #define SWAP (x,y,t) ((t) = (x), (x) = (y), (y) = (t))

    typedef struct {
        int key;
    } element;
    
    void adjust(element a[], int root, int n)
    {
        int child, rootkey;
        element temp;
        temp = a[root];
        rootkey = a[root].key;
        child = 2 * root; /* left child */
        
        while(child <= n) {
            if ((child < n) && (a[child].key < a[child+1].key))
                child++;
                
            if (rootkey > a[child].key) /* compare root and max. child */
                break;
            else {
                a[child / 2] = a[child]; /* move to parent */
                child *= 2;
            }
        }
        a[child / 2] = temp;
    }
    
    void heapInitialization(element a[], int n)
    {
        int i;
        element temp;

        for (i = n/2; i > 0; i--)
            adjust(a, i, n);
    }
    
    void heapSort(element a[], int n)
    {
        int i;
        element temp;
        
        for (i = n-1; i > 0; i--) {
            SWAP(a[1], a[i+1], temp);
            adjust(a, 1, i);
        }
    }

參考解答：(a) $O(logn)$ (b) $O(n)$ (c) $O(nlogn)$

---

10. (6%) Let n be an integer, and S be a set of integers, with range from 1 to $n^2.$ It is known that S has at least $\sqrt{n}$ items. Explain in details how to sort S in $O(|S|)$ time.

參考解答：
利用radix sort
Pass 1: 針對 $key \, i \% \sqrt{n}$
Pass 2: 針對 $[key \, \dfrac{i}{\sqrt{n}}] \% \sqrt{n}$
Pass 3: 針對 $[key \, \dfrac{i}{n}] \% \sqrt{n}$
Pass 4: 針對 $[key \, \dfrac{i}{n \sqrt{n}}] \% \sqrt{n}$
Total time: $4 \times O(\sqrt{n}) = O(\sqrt{n})$

---

11. (4%)

(a) Explain why it takes at least 4 comparisons, in the worst case, to sort four distinct numbers.
(b) Show how to sort four distinct numbers with at most 4 comparisons.

參考解答：
(a)
用decision tree, 所有比較結果 = leaf數 = $4!$
$2^h \geq 4! \to h \geq lg4! > 4,$ 取$h = 5 \to$ 樹高等於5（比較4次）
(b) 把decision tree畫出來

---

12. (7%)

(a) Let S be a set of n positive integers, and we are interested if we can select some of the integers from S so that their sum is exactly m, Explain in detail how this can be done in $O(nm)$ time.
(b) The above problem is called a subset sum problem, which is NP-hard. So far, no polynomial-time algorithms are known to solve an NP-hard problem. Explain why an $O(nm)$-time algorithm is not considered as a polynomial-time algorithm for the subset sum problem.

參考解答：
(a)
使用dynamic programming令$S(i,j)$表$a_1 ~ a_i$中可取出$\text{sum} = j.$
$
\begin{equation}
\begin{cases}
S(i,j) = S(i-1,j) \text{ or } S(i-1,j-w_i)\\
S(0,j) = 0\\
S(i,0) = 1
\end{cases}
\end{equation}
$
更新此matrix需$O(nm)$
(b) $m$需用$2^k$個bits存，因此時間複雜度為$O(2^k \times n)$ not polynomial.

---

13. (6%) Testing gifted or mediocre: m students take an exam which has n questions. Gifted students get all n answers right. Mediocre students get less than n/2 answers right. Grade all the exams, giving all gifted students an ‘A’ and all mediocre students a ‘C’.

Algorithm 1:
1. For each student, grade at most the first n/2 questions in order – stop as soon as you see a wrong answer.
2. If you’ve seen a wrong answer, give grade ‘C’. Otherwise give grade ‘A’.
Algorithm 2:
1. For each student, choose 10 questions at random and grade them.
2. If you’ve seen a wrong answer, give grade ‘C’. Otherwise give grade ‘A’.
Algorithm 3:
1. For each student, repeatedly choose a question at random and grade it, until you have graded n/2 correct answers or seen a wrong answer.
2. If you’ve seen a wrong answer, give grade ‘C’. Otherwise give grade ‘A’.

Explain the correctness and the running time of these three algorithms.

	Algorithm 1	Algorithm 2	Algorithm 3
Correctness	(a)	(b)	(c)
Running time	(d)	(e)	(f)

參考解答：(a) wrong (b) wrong (c) wrong (d) $O(nm)$ (e) $O(m)$ (f) $O(nm)$

---

14. (6%)

(a) What is an optimal Huffman code for the set of frequencies, $\{1,1,2,3,5,8\},$ based on the first six Fibonacci numbers?
(b) Generalize your answer to find the optimal code when the frequencies are the first n Fibonacci numbers.

參考解答：
(a)
Fib[1] = 11111
Fib[2] = 11110
Fib[3] = 1110
Fib[4] = 110
Fib[5] = 10
Fib[6] = 0
(b)
Fib[1] = 111…11 (n-1個1)
Fib[2] = 111…10 (n-2個1)
Fib[3] = 11…10 (n-3個1)
.
.
.
Fib[n] = 0

---

15. (5%) The constrained 1-center problem: Given n planar points and a straight line L, find a smallest circle, whose center is restricted to lying on L, to cover these n points. The following lists an algorithm for solving this problem. Evaluate the time complexity, $T(n),$ of this algorithm using the recurrence relation of $T(n).$

Input: n points and a straight line $L:y = y’.$
Output: The constrained 1-center on L.

Step 1. If n is no more than 2, solve this problem by a brute-force method.
Step 2. Form disjoint pairs of points $(p_1,p_2),(p_3,p_4),…,(p_{n-1},p_n).$ If n is odd, let the final pair be $(p_n,p_1).$
Step 3. For each pair of points, $(p_i,p_{i+1}),$ find the point $x_{i,i+1}$ on L such that $d(p_i,x_{i,i+1}) = d(p_{i+1},x_{i,i+1}).$
Step 4. Find the median of the $\lceil n/2 \rceil$ numbers of $x_{i,i+1}$’s. Denote it as $x_m.$
Step 5. Calculate the distance between $p_i$ and $x_m$ for all i. Let $p_j$ be the point which is the farthest from $x_m.$ Let $x_j$ denote the projection of $p_j$ onto L. If $x_j$ is to the left (right) of $x_m,$ then the optimal solution, $x^*,$ must be to the left (right) of $\lambda_m.$
Step 6. If $x^* < x_m,$ for each $x_{i,i+1} > x_m,$ prune the point $p_i$ if $p_i$ is closer to $x_m$ than $p_{i+1};$ otherwise prune the point $p_{i+1}.$ If $x^* > x_m,$ for each $x_{i,i+1} < x_m,$ prune the point $p_i$ if $p_i$ is closer to $x_m$ than $p_{i+1};$ otherwise prune the point $p_{i+1}.$
Step 7. Go to step 1.

參考解答：$T(n) = T(\dfrac{3n}{4}) + O(n).$ Time Complexity: $O(n).$

---

試題(pdf)：連結

有任何問題，或想要完整解釋的，歡迎在下方留言唷！