105成大資聯離散[參考解答]

1. For $n \geq 1,$ let $a_n$ count the number of ways to write $n$ as an ordered sum of odd positive integers. (For example, $a_4 = 3$ since 4 = 3+1 = 1+3 = 1+1+1+1.) Find and solve a recurrence relation for $a_n.$ (15%)

參考解答：$a_n = a_{n-1} + a_{n-2}, \, \forall n \geq 3. \ a_1 = 1, \, a_2 = 1.$

---

2.

(a) How many bit strings of length 8 do not contain three consecutive 1s? (10%)
(b) What is the probability that a ternary sequences (sequence made up of the digits 0, 1, 2) of length 8 contains even number of 1’s bits? (10%)

參考解答：
(a) $149$
(b) $\dfrac{3281}{3^8}$

---

3. Let $p, \, q$ be two distinct primes. We denote relation $x R y$ if $x$ divides $y.$ Under this relation $R,$ please determine (a) the Hasse diagram of all positive divisors of $p^2q^2,$ (b) $glb\{pq, \, p^2\},$ (c) How many edges are there in the Hasse diagram of all positive divisors of $p^mq^2, \, m \in Z^+.$ (15%)

參考解答：
(a)

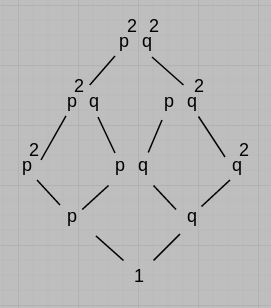
(b) $p$
(c) $5m + 2$

---

試題(pdf)：連結

有任何問題，或想要完整解釋的，歡迎在下方留言唷！