1. (10%) Given an array A (as shown below), which represents a complete binary tree, answer the following three questions.
| i | 1 | 2 | 3 | 4 | 5 | 6 |
| A[i] | 5 | 15 | 10 | 34 | 29 | 28 |
(1) Draw the corresponding binary tree T.
(2) Does the tree satisfy the heap property? If so, what kind of heap structure is it?
(3) Perform the following heap operations sequentially: INSERT(19), INSERT(7), INSERT(60). If we use an array to represent the tree, show how the array looks like after the operations.
參考解答:
(1)
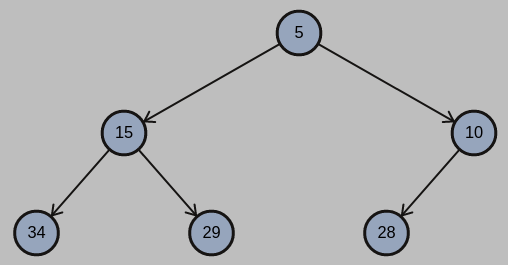
(2) Yes, is a min-heap.
(3)
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| A[i] | 5 | 7 | 10 | 15 | 29 | 28 | 19 | 34 | 60 |
2. (10%) Answer the following questions about AVL trees:
(1) Which of the following statement(s) about AVL trees are true?
(A) AVL trees are binary trees.
(B) AVL trees are heap structures.
(C) AVL trees are ideal for storing items of an ordered dictionary.
(D) AVL trees satisfy the height-balance property.
(2) Which of the following statement(s) about the complexity of AVL trees are true?
(A) The space complexity of AVL trees is $O(n)$
(B) The time complexity for searching an item in an AVL tree is $O(nlogn)$
(C) The time complexity for removing an item from an AVL tree is $O(n)$
(D) The time complexity for inserting an item into an AVL tree is $O(logn)$
(3) Let $N_h$ represent the minimum number of nodes that can form an AVL tree of height h. $N_1 = 1, \text{ and } N_2 = 2.$ Show what’s the height of AVL trees with n nodes for $h \geq 3$ using Big-O notation. Show how to derive your answer.
參考解答:(1) ACD (2) AD (3) $N_h = N_{h-1} + N_{h-2} + 1 = O((\dfrac{1 + \sqrt{5}}{2})^h)$
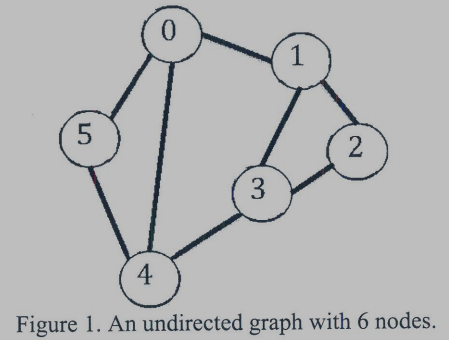
3. (10%) Consider the undirected graph shown in Figure 1.
(1) What is the adjacency matrix representation of this graph?
(2) What is the adjacency list representation of this graph?
(3) Assume that the cost of the edge linking node u and node v is max(u,v). Use Kruskal’s algorithm to find a minimum cost spanning tree of this graph.
參考解答:
(1)
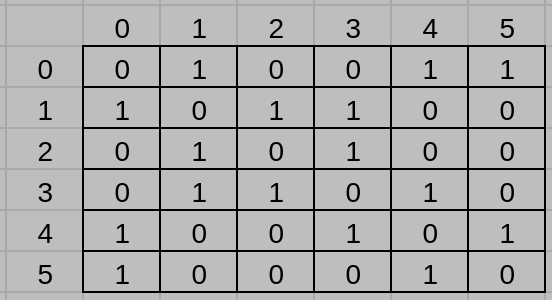
(2)

(3)
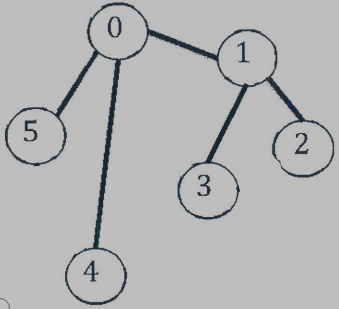
Minimum cost: 15
4. (10%) Consider the hash table ht with b=26 buckets. Each bucket can hold s=2 slots. We have n=10 distinct identifiers, each representing a networking device or networking entity. The hash function must map each of the possible identifiers onto one of the numbers, 0-25. Using a hash function, we hash the identifiers router, packet, TCP, broadcast, ARP, VLAN, HTTP, IP, DHCP, and BCMP into buckets 0, 3, 5, 4, 2, 0, 2, 5, 2, and 2, respectively.
(1) What is the loading factor of this hash table?
(2) Explain what an overflow is? Do overflows occur in this hash table? If so, when does the first overflow occur in this table?
(3) Which one of the following is a method of solving overflow problems? Division, mid-square, folding, and chaining?
參考解答:
(1) $\dfrac{5}{26}$
(2) When there is a collision and the corresponding bucket doesn’t have more free slots. Yes, the first overflow occurs in bucket 2 when inserting DHCP.
(3) Chaining
5. (10%) Which ones of the following conjectures are correct? Please justify your answers:
(A) $3n^2 – 100n + 6 = O(n)$
(B) $lg(n!) = \Theta(nlgn)$
(C) $n! = O(n^n)$
(D) $(n + a)^b = \Theta(n^b),$ a and b are real constants.
(E) $(n + a)^b = \Omega(n^{b+1})$
參考解答:BCD
6. (10%) Assume Alex and Bella need to write some programs to deal with certain data sets for their customers. Alex decides to use Merge Sort for ASuperStar Company. Bella decides to use Bucket Sort for BrilliantGenius Company. Both ASuperStar and BrilliantGenius are happy for the delivered product. These two companies believe their corresponding programmers (i.e., Alex and Bella) made the best decision during the development.
Please describe the possible data characteristics for ASuperStar and Brilliant Genius based on the choices of Alex and Bella.
參考解答:
ASuperStar: Since Alex decides to use Merge Sort, it’s very likely that their data are not in a specific range, in other words, they have all data in random places. (Comparison-based)
BrilliantGenius: Since Bella decides to use Bucket Sort, it’s very likely that their data are in a specific range. (Counting-based)
7. (12%) Determine whether the following statements are correct or not and also justify your reasons. No points for answers without justification.
(1) An NP-complete problem is also an NP-hard problem.
(2) The complexity class NP is the class of languages that cannot be solved by any polynomial-time algorithm.
(3) To prove that a decision problem X is NP-complete, we need to 1) show that X is in NP, and 2) reduce X to any known NP-complete problem.
(4) There exists a 3-approximation algorithm for TSP (Travelling Salesman Problem).
參考解答:(1) T (2) F (3) F (4) F
8. (8%) Given a graph G=(V,E), a subset of vertices $S \subseteq V$ is said to be a k-plex if the minimum degree of the subgraph induced by S on G is at least $|S| – k.$ For example, $S = {a,b,c,d,e}$ is a 3-plex with $|S| = 5.$ In contranst, $S^* = {a,b,c,d,e,f}$ is not a 3-plex.
(1) The k-plex problem is defined as follows: Given a graph G=(V,E), positive integers k and p, does G contain a subset of vertices S suck that $|S| = p$ and S is a k-plex? Either provide a polynomial time algorithm to solve the k-plex problem or prove that this problem is NP-hard.
(2) Given a k-plex S and any nonempty subset $S’ \subseteq S, \text{ is } S’$ also a k-plex? If yes, please provide the proof. If no, please provide a counterexample.
參考解答:
(1)

(2)

9. (10%) A computer prints all bit strings of length 9.
(1) How many begin with 01 or end with 10?
(2) How many have either five consecutive 1s or five consecutive 0s?
(3) How many have exactly three 1s and none of these 1s are adjacent to each other? And how many have three 1s and six 0s?
參考解答:(1) 224 (2) 96 (3) 35, 84.
10. (10%) Use generating functions to answer the following questions.
(1) Find the coefficients of $x^9$ in the power series of the function: $\dfrac{1}{1 + 3x}.$
(2) Find an explicit formula for the recurrence relation $a_k = 5a_{k-1} – 6a_{k-2}$ with initial conditions $a_0 = 1 \text{ and } a_1 = 5.$
參考解答:(1) $-3^9$ (2) $a_n = -2 \cdot 2^n + 3 \cdot 3^n, \, n \geq 0.$
試題(pdf):連結
有任何問題,或想要完整解釋的,歡迎在下方留言唷!





pan
https://i.imgur.com/iV0GmpM.jpg
mt
感謝提供第八題的答案~
Jackson
你好請問 load factor 是怎麼計算呢?
我看定義是說在 capacity 增加前之附載量
The load factor is a measure of how full the hash table is allowed to get before its capacity is automatically increased. 謝謝
mt
loading factor我是用“elements數量除以slots數量”喔
10/(26*2)=5/26