107成大資聯程設[參考解答]

一、Data Structures (50%)

1. (10%) Suppose that we have numbers between 1 and 1000 in a binary search tree, and we want to search for the number 363. Which of the following sequences could not be the sequence of nodes examined?

(a) 2, 252, 401, 398, 330, 344, 397, 363.
(b) 924, 220, 911, 244, 898, 258, 362, 363.
(c) 925, 202, 911, 240, 912, 245, 363.
(d) 2, 399, 387, 219, 266, 382, 381, 278, 363.
(e) 935, 278, 347, 621, 299, 392, 358, 363.

參考解答：c, e.

---

2. (10%) Compute the minimum weight spanning tree and its cost of the following graph.

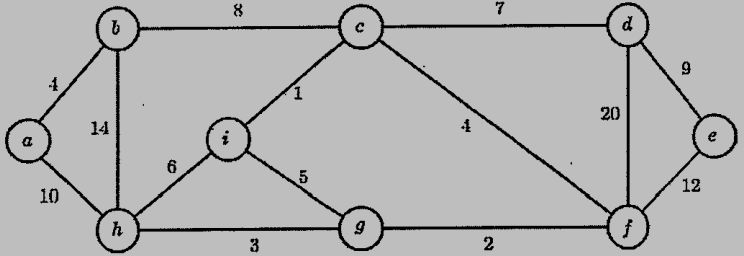
參考解答：38

---

3. (10%) Please write down the adjacency matrix of the following graph in the following table.

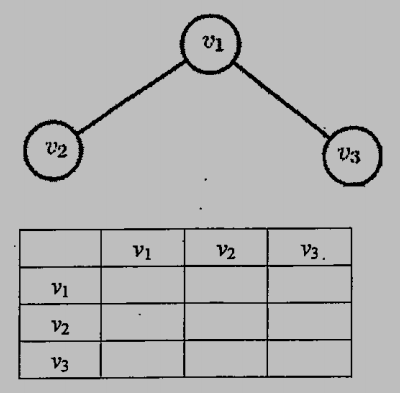
參考解答：

	$v_1$	$v_2$	$v_3$
$v_1$	0	1	1
$v_2$	1	0	0
$v_3$	1	0	0

---

4. (10%) Please compute the total cost of executing n of the stack operations (PUSH, POP, and MULTIPOP).

Stack Operations: PUSH, POP, and MULTIPOP.
PUSH(S,x) pushes object x onto stack S.
POP(S) pops the top of stack S and returns the popped object. Calling POP on an empty stack generates an error.
MULTIPOP(S,k) removes the k top objectives of stack S, popping the entire stack if the stack contains fewer than k objects. The following pseudo code presents the procedure of the MULTIPOP operation.

MULTIPOP(S,k):

while not STACK-EMPTY(S) and k > 0

    POP(S)

    k = k - 1

Both PUSH and POP take $O(1)$ time. The cost of MULTIPOP(S,k) is $1 + min(s,k)$ where s is the number of objects in stack S.
Suppose that there are n stack operations (PUSH, POP, and MULTIPOP) executed.
The stack is empty before those operations start and it is empty after those operations finished.

參考解答：Amortize cost: $O(n)$

---

5. (10%) What is the maximum numbers of elements in a heap of height h?

參考解答：$2^h – 1$

---

二、Algorithms (50%)

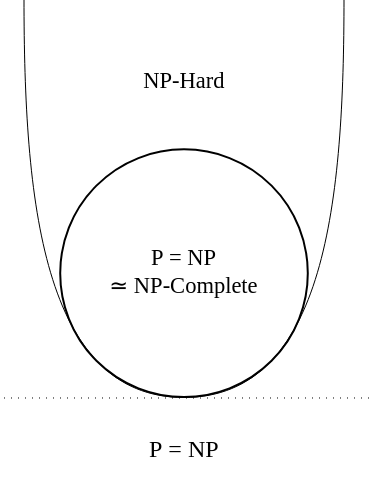
1. (10%) If someone gives a polynomial algorithm for an NP-hard problem, what conclusions you can draw from this fact?

參考解答：

---

2. (10%) Given a sequence of n numbers, what is the lower bound of sorting algorithms using comparison and exchange operations?

參考解答：$\Omega(nlgn)$

---

3. (10%) The following graph is a maximum flow problem. Each edge is labeled with its capacity. What is the maximum flow from vertex s to vertex t.

參考解答：Maximum flow: 23

---

4. (10%) Use master theorem to solve the recurrence $T(n) = 3T(2n/3) + O(1).$

參考解答：$\Theta(n^{log_{\frac{3}{2}}3})$

---

5. (10%) Given a graph $G=(V,E),$ a vertex cover $C \subseteq V$ is a vertex subset, such that if $(u,v) \in E,$ then $u \in C$ or $v \in C.$ The minimum vertex cover problem is to find a vertex cover $C^*$ of $G$ with the minimum cardinality. The following algorithm is a $\delta$-approximation algorithm to find a vertex cover $C$ satisfying $|c| \leq \delta \cdot |C^*|.$ Please compute the minimum value of $\delta.$

APPROX_VERTEX_COVER(G):

C <- 0

E' <- E(G)

while E' != 0

    do let (u,v) be an arbitrary edge of G

        C <- C union {u,v}

        remove from E' every edge incident on either u or v

return C

參考解答：2

---

試題(pdf)：連結

有任何問題，或想要完整解釋的，歡迎在下方留言唷！