1. (12%)
(a) How many integer solutions of $x + y + z \leq 15$ satisfy $x \geq 0, \, y \geq 3, \, z \geq 5?$
(b) In how many ways can we select three distinct integers from 1 to 29 such that their sum is a multiple of 3?
參考解答:
(a) $\binom{4+7-1}{7} = \binom{10}{7} = 120$
(b) 84 + 900+ 120 + 120 = 1224
2. (8%) A tree T has 2n vertices of degree 1, 3n vertices of degree 2, and n vertices of degree 3.
(a) Determine the value of n.
(b) What is the minimum number of edges that can be added to T so that the resultant graph will have an Euler circuit?
參考解答:(a) n = 2 (b) 3
3. (10%) Given a $k \in Z^+,$ the number of derangements $d_k$ is defined as the number of arrangements of $1,2,…,k$ where none of the numbers $1,2,…,k$ are in their natural position. Take $k = 4$ as an example, 4,3,2,1 is considered as one of the dearrangements. We define $d_0 = 1$ for convenience.
For all $n \in Z^+,$ use combinatorial arguments to prove the following equation $n! = \binom{n}{0}d_0 + \binom{n}{1}d_1 + … + \binom{n}{n}d_n = \sum_{k=0}^n \binom{n}{k}d_k.$
Remarks: No marks will be given if your proof is not a combinatorial one.
參考解答:
考慮n個數作排序,共$n!$種可能,可分成以下幾種情形:
假設有n個數在自然位置上,則剩餘0個人不在自然位置上,方法數為$\binom{n}{0}d_0$
假設有n-1個數在自然位置上,則剩餘1個人不在自然位置上,方法數為$\binom{n}{1}d_1$
假設有n-2個數在自然位置上,則剩餘2個人不在自然位置上,方法數為$\binom{n}{2}d_2$
…
假設有0個數在自然位置上,則剩餘n個人不在自然位置上,方法數為$\binom{n}{n}d_n$
所以n個數作排序之方法數為
$$n! = \binom{n}{0}d_0 + \binom{n}{1}d_1 + \binom{n}{2}d_2 + … + \binom{n}{n}d_n = \sum_{k=0}^n \binom{n}{k}d_k$$
4. (10%) On the set $Z,$ define relation $R \text{ by } aRb \text{ if } a-b$ is a nonnegative even integer.
(a) Prove or disprove that $R$ is a partial order on $Z$.
(b) Prove or disprove that $R$ is a total order on $Z$.
Remark: No marks will be given if you do not show your work.
參考解答:
(a)
$\forall a \in Z,$ 因為$a – a = 0$為非負偶數,所以$aRa,$ 因此$a$具reflexive.
$\forall a, \, b \in Z,$ 假設$aRb \text{ 且 } bRa,$ 則$a – b \geq 0 \text{ 且 } b – a \geq 0 \to a = b,$ 所以$R$具antisymmetric.
$\forall a, \, b, \, c \in Z,$ 假設$aRb \text{ 且 } bRc,$ 則存在$k_1, \, k_2$為非負整數使得$a – b = 2k_1 \geq – \text{ 且 } b – c = 2k_2 \geq 0 \to a – c = (a – b) + (b – c) = 2k_1 + 2k_2 = 2(k_1 + k_2) \geq 0 \to aRc,$ 所以$R$具transitive.
因此$R$為partial order on $Z.$
(b) 取$a = 1, \, b = 2 \in Z,$ 因為$(a,b) \notin R \text{ 且 } (b,a) \notin R,$ 所以$R$不為total order on $Z.$
5. (6%) Please answer whether each of the following statements is correct.
(a) $logn \text{ is in } O(n^{0.1}).$
(b) $n! + n^n \text{ is in } \Theta(n^n).$
(c) $2^n + n^n \text{ is in } \Theta(2^n).$
(d) $n! \text{ is in } \Omega(2^n).$
(e) $2^n \text{ is in } O(n^{100}).$
(f) $nlogn \text{ is in } \Omega(n^2).$
參考解答:(a) T (b) T (c) F (d) T (e) F (f) F
6. (6%)
(a) Please draw the graph with the following sequential representation.

(b) Please draw the graph with the following representation of adjacency multilists.
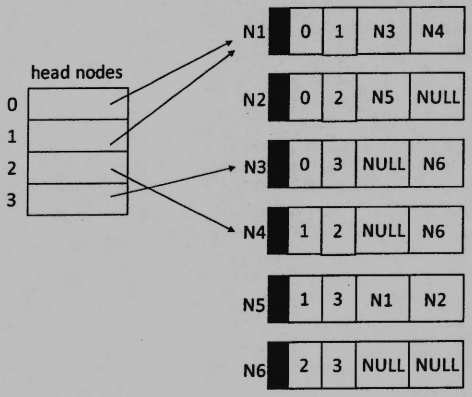
參考解答:
(a)
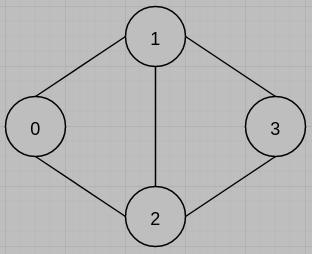
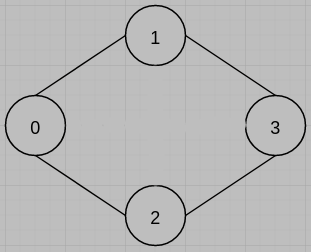
(b)
7. (18%)
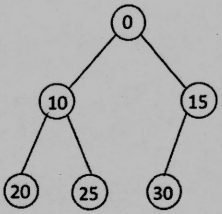
(a) Please draw the min heap (shown as follows) following a delete min.
(b) Please draw the min-max heap (shown as follows) following a delete min.
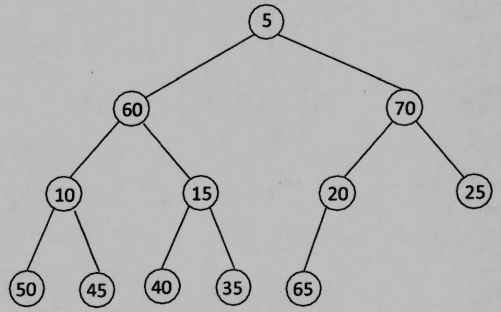
(c) Please draw the deap (shown as follows) following a delete min.
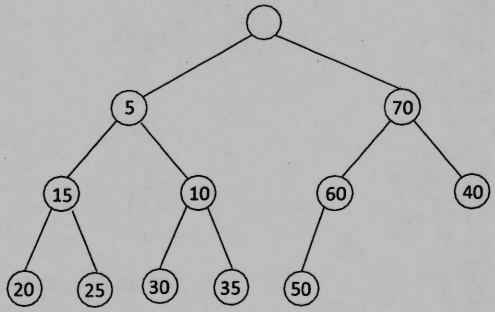
(d) Please draw the min leftist tree (shown as follows) following a delete min.
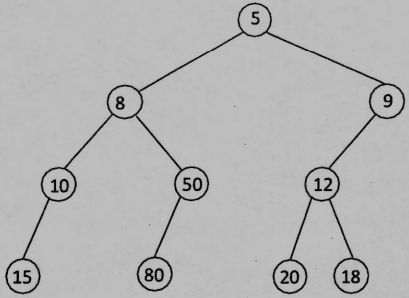
(e) Please draw the 2-3-4 tree (shown as follows) following the deletion of 15.
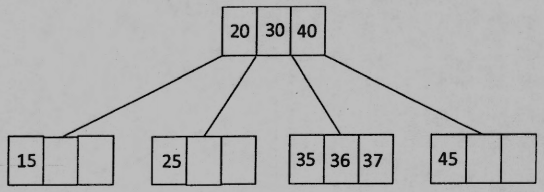
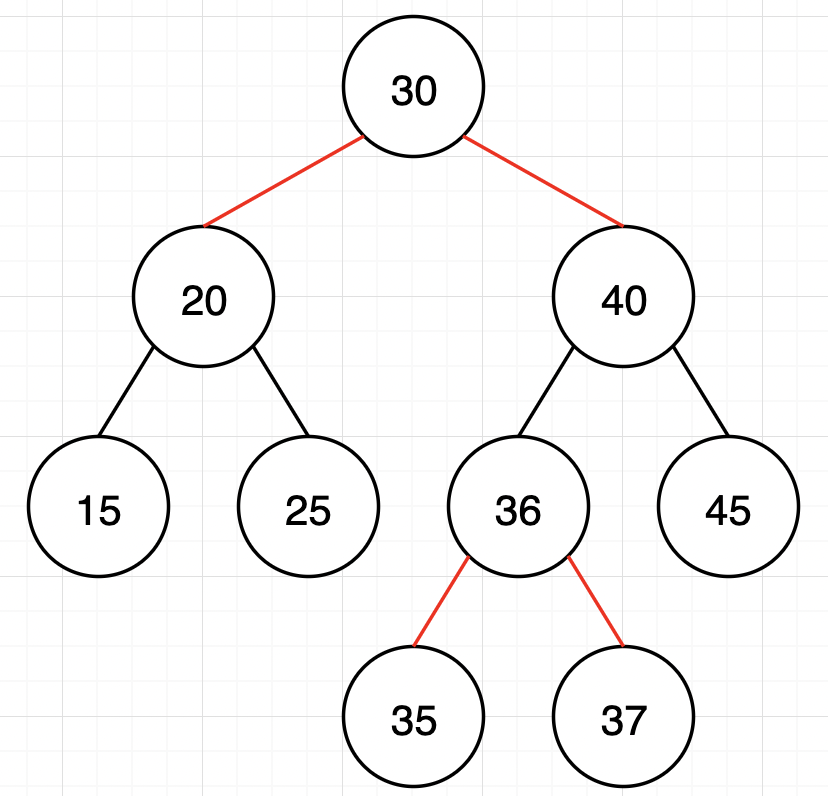
(f) Please draw the red-black representation of 2-3-4 tree shown in (e).
參考解答:
(a)
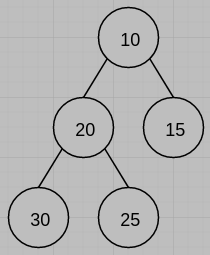
(b)
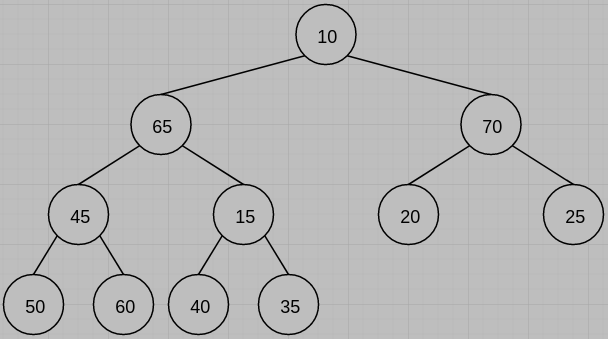
(c)
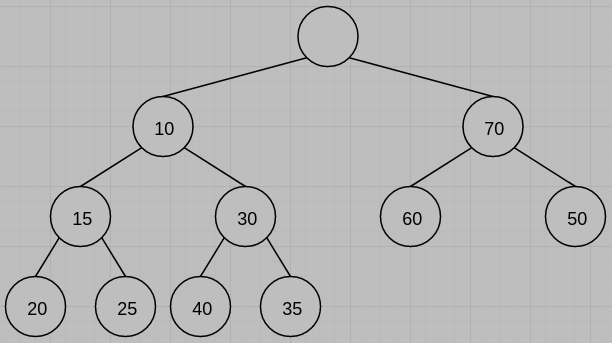
(d)
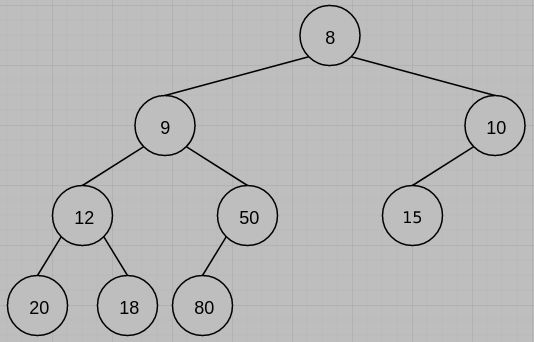
(e)
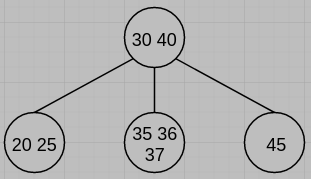
(f)
8. (30%) For an input connected undirected graph G,
- the HP problem asks if G contains a Hamiltonian path; and
- the HC problem asks if G contains a Hamiltonian circuit.
(a) Describe a polynomial-time reduction from HP to HC, and explain why such a reduction works.
(b) Describe a polynomial-time reduction from HC to HP, and explain why such a reduction works.
Remark: No marks may be given if the reduction does not work, or the explanation is incomplete.
參考解答:略
試題(pdf):連結
有任何問題,或想要完整解釋的,歡迎在下方留言唷!





Jackson
您好,想問畫圖7(d) node 10 左子應該是 15 不是 5 吧?
還有 7(f) 不是指畫原圖的意思嗎? 謝謝
mt
對誒~7(d)錯了,然後7(f)應該是要畫原本的圖沒錯,感謝提醒。
Mason
不好意思 想請問一下 第6題的 (b) 小題,N2 跟 N5 好像不會Linked 到,所以1 與 3、0 與 2的點應該不會相連 !? 不知道是不是我會錯意了,感謝指教~~
mt
你說的沒錯喔~感謝提醒!