1. (15%) Consider the set $S = \{a,b,c,d,e\},$ and a logical matrix $M$ corresponding to a relation $R$ on the set $S$ is shown in the following.
$$
M =
\begin{bmatrix}
1 & 0 & 1 & 0 & 0\\
0 & 1 & 0 & 0 & 0\\
0 & 0 & 1 & 0 & 0\\
1 & 1 & 1 & 1 & 1\\
0 & 1 & 1 & 0 & 1
\end{bmatrix}
$$
(a) In order to check if there exists a partial ordering, which properties should you check?
(b) Draw the Hasse diagram of this order.
(c) Determine all pairs of incomparable elements.
參考解答:
(a) 1. Reflexive 2. Anti-symmetric 3. Transitive
(b)
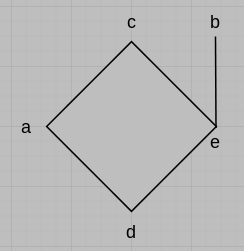
(c) (a, b), (a, e), (b, c).
2. (15%) Solve the following recurrence equations for $A(n),$ and $B(n).$
$$
\begin{equation}
\begin{cases}
A(n) = 3A(n-1) + 2B(n-1)\\
B(n) = A(n-1) + B(n-1)\\
n \geq 1, A(0) = \sqrt{3}, B(0) = 0
\end{cases}
\end{equation}
$$
參考解答:$A(n) = \dfrac{1}{2}[(1 + \sqrt{3})(2 + \sqrt{3})^n + (-1 + \sqrt{3})(2 – \sqrt{3})^n] \ B(n) = \dfrac{1}{2}[(2 + \sqrt{3})^n – (2 – \sqrt{3})^n]$
3. (20%) Given the following figures (a) and (b). Assume the source node is a and the sink node is f. The label along the edge (or node) means the maximum capacity of the edge (or node).

(a) Find the maximum flow from the source to the sink. And what is the corresponding minimum cut in Fig. (a).
(b) Find the maximum flow from the source to the sink. And what is the corresponding minimum cut in Fig. (b).
參考解答:
(a) Max flow: 8, $\{\{a,b,c,d,e\},\{f,g,h,i,j\}\} \in \text{min-cut}.$
(b) Max flow: 15
試題(pdf):連結
有任何問題,或想要完整解釋的,歡迎在下方留言唷!





發佈留言