1. (10%) Use generating functions to answer the following questions.
(A) Find the solution of the recurrence relation $a_n = 4a_{n-1} – 3a_{n-2} + 2^n + n + 3 \text{ with } a_0 = 1 \text{ and } a_1 = 4.$
(B) Find the coefficient of $x^{10}$ in the power series of $x^4 / (1 – 3x)^3.$
參考解答:
(A) $a_n = -4 \cdot 2^n + \dfrac{39}{8} \cdot 3^n + \dfrac{19}{8} – \dfrac{7}{4}(n+1) – \dfrac{1}{4}(n+2)(n+1), \, n \geq 0.$
(B) $\binom{3+6-1}{6} \cdot 3^6 = 28 \cdot 3^6 = 20412$
2. (10%) How many relations are there on a set with n elements that are
(A) both reflexive and symmetric?
(B) neither reflexive nor irreflexive?
參考解答:
(A) $2^{\frac{n(n-1)}{2}}$
(B) $2^{n^2} – 2^{n(n-1)+1}$
3. (5%) How many nonisomorphic unrooted trees are there with five vertices?
參考解答:3
4. (5%) Multiple answer question. (It is possible that more than one of the choices are correct. Find out all correct choices.)
A hash table of length 10 uses the hash function $h(k) = k \, mod \, 10$ and the linear probing for handling overflow. After inserting 6 values into an initially empty hash table, the table is as shown below. Which one(s) of the following choices gives a possible order in which the key values could have been inserted in the table?
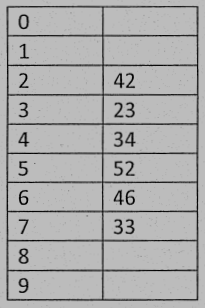
(A) 46, 42, 34, 52, 23, 33
(B) 34, 42, 23, 52, 33, 46
(C) 46, 34, 42, 23, 52, 33
(D) 42, 46, 33, 23, 34, 52
(E) 42, 23, 34, 46, 52, 33
參考解答:CE
5. (5%) Fill in the six black (I, II, …, and VI) in the following program that implements a queue by using 2 stacks.
class MyQueue<T> {
private:
stack<T> stack1;
stack<T> stack2;
public:
MyQueue()
{
stack1 = new stack<T>();
stack2 = new stack<T>();
}
// enqueue(): Add an element at the rear side of MyQueue
void enqueue(T, e)
{
stack1.push(e);
}
// dequeue(): Remove the front element from MyQueue
T dequeue(T, e)
{
if((__I__).isEmpty())
while(!(__II__).isEmpty())
(__III__).push((__IV__).pop());
T temp = null;
if(!(__V__).isEmpty())
temp = (__VI__).pop();
return temp;
}
}參考解答:(I) stack2 (II) stack1 (III) stack2 (IV) stack1 (V) stack2 (VI) stack2
6. (5%) AVL Tree.
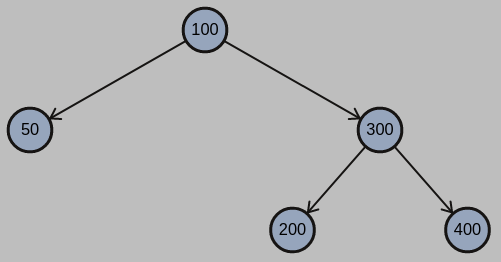
(A) Please draw how an initially-empty AVL tree would look like after sequentially inserting the integer keys 100, 200, 50, 300, 400. There is no need to show it in a step-by-step fashion; you only need to draw the final result.
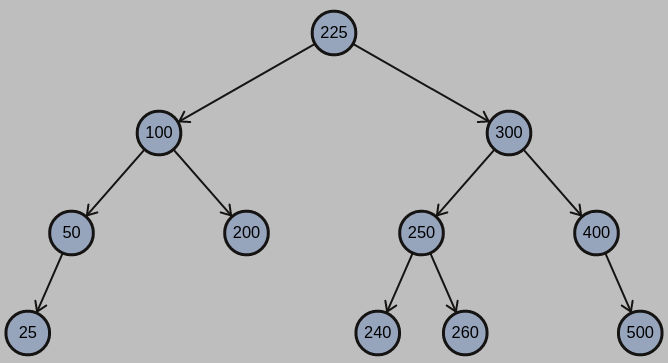
(B) Continue the previous sub-problem. Suppose that the integer keys 25, 250, 225, 500, 240, 260 are sequentially inserted into the AVL tree of the previous sub-problem. Draw the AVL tree after all of these integer keys are inserted.
參考解答:
(A)
(B)
7. (5%) Reconstruct and draw the maximum binary heap whose in-order traversal is 2, 16, 7, 62, 5, 9, 188, 14, 78, 10. There is no need to show it in a step-by-step fashion; you only need to draw the final result.
參考解答:
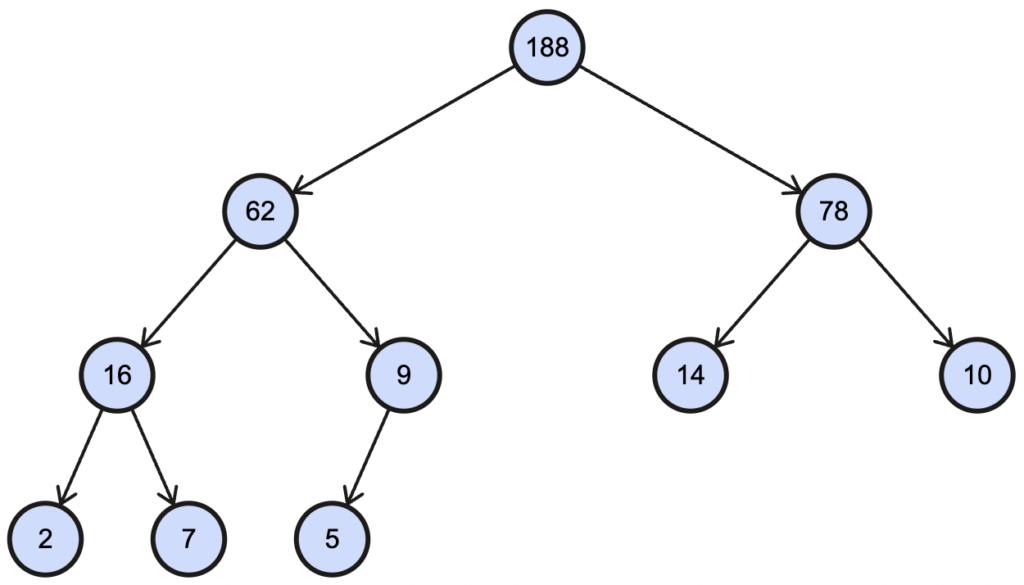
8. (5%) The following algorithm takes an array as input and returns the array with all the duplicate elements removed. For example, if the input array is {1, 3, 3, 2, 4, 2}, the algorithm returns {1, 3, 2, 4}.
S = new empty set
A = new empty dynamic array
for every element x in input array
if not S.member(x) then
S.insert(x)
A.append(x)
return ASuppose that the input array has n elements. What is the Big-O complexity of this algorithm, if the set S is implemented as:
(A) a hash table (with the assumption that overflow does not occur)?
(B) a binary search tree?
(C) an AVL tree?
參考解答:(A) $O(n)$ (B) $O(n^2)$ (C) $O(nlgn)$
9. (10%) The recurrence $T(n) = 7T(\dfrac{n}{2}) + n^2$ describes the running time of an algorithm A. A completing algorithm A’ has a running time of $T'(n) = aT'(\dfrac{4}{n}) + n^2.$ What is the largest integer value for $a$ such that A’ is asymptotically faster than A?
參考解答:48
10. (15%) Consider the following undirected graph G = (V,E).
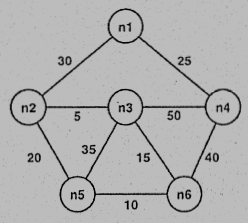
(A) Draw the process of finding a minimum spanning tree using Kruskal’s algorithm.
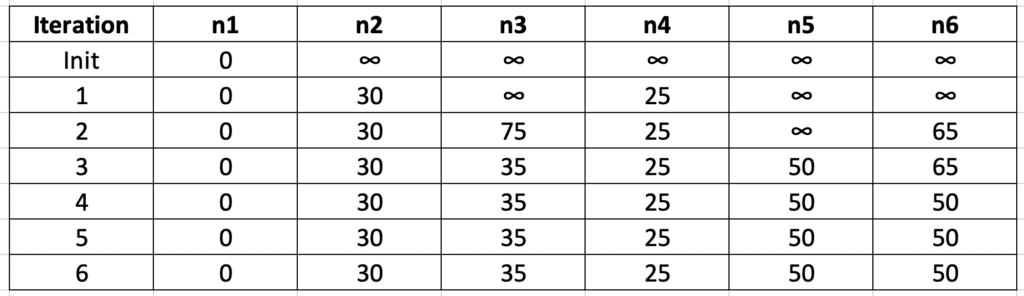
(B) Draw the process of solving the single-source shortest path problem with node n1 as the source vertex using Dijkstra’s algorithm.
(C) Starting from n1, find the Depth-First Search (DFS) traversal sequence of G (the priority of node is inversely proportional to the weight of incident edge).
參考解答:
(A)
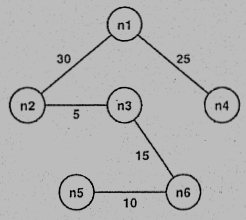
(B)
(C) $n1 \to n4 \to n6 \to n5 \to n2 \to n3$
11. (18%) Given an ordered file with keys 1, 2, …, 16, determine the number of key comparisons made by a search algorithm A while searching for a specific key K.
(A) A is the binary search algorithm and K is 2.
(B) A is the binary search algorithm and K is 10.
(C) A is the binary search algorithm and K is 15.
(D) A is the Fibonacci search algorithm and K is 2.
(E) A is the Fibonacci search algorithm and K is 10.
(F) A is the Fibonacci search algorithm and K is 15.
參考解答:(A) 3 (B) 3 (C) 4 (D) 4 (E) 3 (D) 5
12. (7%) Given a store of n items, what’s is the least upper bound (in Big-O notation) of the running time of the solutions to the following problems:
(A) Fractional knapsack problem;
(B) General 0/1 knapsack problem.
參考解答:(A) $O(nlgn)$ (B) $O(nW),$ where W is the bag weight value.
試題(pdf):連結
有任何問題,或想要完整解釋的,歡迎在下方留言唷!





流動性
您好,我想知道第11題的DEF小題您在fibonacci search的求解過程是如何呢?因為我在網路上爬文有找到一篇討論的答案和這裡不一樣,謝謝!
以下是我找到的討論:
https://www.pttweb.cc/bbs/Grad-ProbAsk/M.1579430402.A.9A2
mt
Fibonacci search的步驟網路上真的有很多版本,解出來的答案也都不太一樣,我自己是用這部影片的方法。所以答案不同有可能是因為方法不一樣,可以去看看那所學校的大學部上課的時候的用書,然後看那本書是用什麼方法,這樣比較保險,加油喔!
w
第七題max heap圖是不是錯了
mt
對!答案已更新,謝謝你。
TNF
請問第八題的A選項
題目是假設沒有overflow的發生
但如果幾乎全部都collision且採linear probing
判斷元素是否在hash table的比較次數變成1+2+…+(n-1)
是否最差時間複雜度就是O(n^2)了呢
另外O(n)是平均狀況嗎??
mt
我這題是假設說每個bucket只有一個slot然後題目又說沒有overflow(等於沒有collision,因為只有一個slot時,collision等於overflow),所以我才寫O(n)。然後就算collision的話也不會overflow所以不會有採用哪種probing的問題,不過這題也可以想成是用chaining,這樣的話是O(n^2)沒錯。希望有回答到你的問題~
aaa
嗨,第10題(b)的第2個iteration的node n3應該是75吧?因為第1個iteration是選node n4,所以更新n3從無限大->75
mt
對誒!謝謝你~