資料結構 (50%)
1. Answer True or False for the following statements. Give correct answers for False statements. (20%)
(1) Let $G$ be a graph with $e$ edges and $v$ vertices. If $G$ is represented by adjacency lists, DFS requires $O(v^2)$ time.
(2) If an AOV network represents a feasible project, its topological order is unique.
(3) In static hashing, the worst-case number of comparisons needed for a successful search is $O(n)$ for open addressing. The number could be reduced to $O(log n)$ by using chaining method.
(4) Let $d_i$ be the degree of vertex $i$ in a graph $G$ with $|V| = n$ and $|E| = e,$ then $e = \sum_{n=0}^{n-1}d_i.$
(5) The path from vertex $u$ to vertex $v$ on a minimal cost spanning tree of an undirected graph $G$ is also a shortest path from $u$ to $v.$
參考解答:(1) F (2) F (3) F (4) F (5) F
2. Given the following 8 runs: (15%)

(1) Draw the corresponding winner tree.
(2) Draw the restructured winner tree after one record has been output.
(3) Draw the loser tree based on the answer of question (2).
(4) Derive the total required time to merge n records through a winner tree with k runs.
參考解答:
(1)

(2)
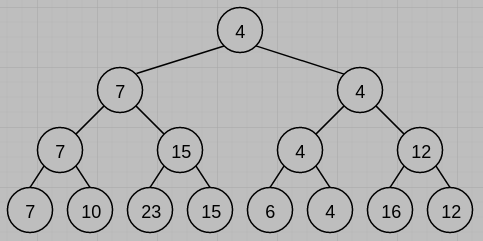
(3)
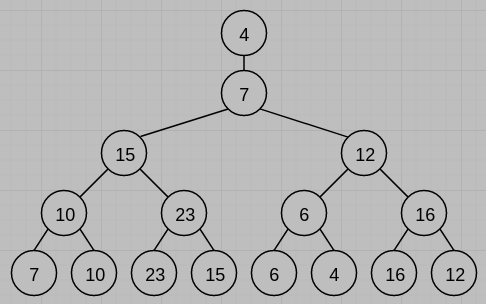
(4) $O(nlgk)$
3. Consider the following AOE network: (15%)
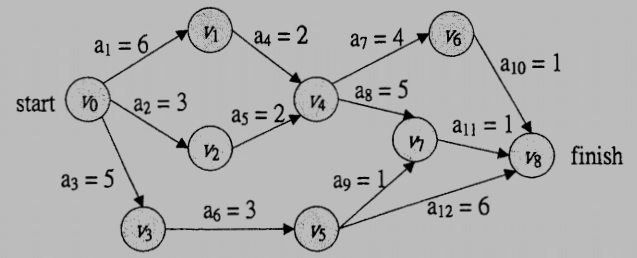
(1) Obtain $e(i)$ and $l(i)$ for all activity $i.$
(2) List all critical activities.
(3) List all critical paths.
參考解答:
(1)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| $e$ | 0 | 0 | 0 | 6 | 3 | 5 | 8 | 8 | 8 | 12 | 13 | 8 |
| $l$ | 0 | 3 | 0 | 6 | 6 | 5 | 9 | 8 | 12 | 13 | 13 | 8 |
(2) $a_1, \, a_3, \, a_4, \, a_6, \, a_8, \, a_{11}, \, a_{12}.$
(3) $v_0 \to v_1 \to v_4 \to v_7 \to v_8 \ v_0 \to v_3 \to v_5 \to v_8$
演算法 (50%)
1. Answer True or False for the following statements. Give correct answers for False statements. (20%)
(1) If P equals NP, then NP equals NP-complete.
(2) Any n-node unbalanced tree can be balanced using $O(logn)$ rotations.
(3) Let $A_1, \, A_2$ and $A_3$ be three sorted arrays of $n$ real numbers (all distinct). In the comparison model, constructing a balanced binary search tree of the set $A_1 \cup A_2 \cup A_3$ requires $\Omega (nlogn)$ time.
(4) Let P be a shortest path from some vertex s to some other vertex t in a graph. If the weight of each edge in the graph is increased by one, P remains a shortest path from s to t.
(5) We can claim that there is a simpler way to reweight edges than the method used in Johnson’s algorithm. Letting $w^* = min_{(u,v) \in E}\{w(u,v)\},$ just define $\hat{w}(u,v) = w(u,v) – w^*$ for all edges $(u,v) \in E.$
參考解答:(1) T (2) F (3) F (4) F (5) F
2. Give a tight asymptotic upper bound on the solution to the following recurrence. (10%)
$$
\begin{equation}
T(n) =
\begin{cases}
16T(\dfrac{n}{2})+\Theta(1) & \text{if $n^2 > M,$}\\
M & \text{if $n^2 \leq M;$}
\end{cases}
\end{equation}
$$
參考解答:$O(\dfrac{n^4}{M})$
3. Prove that the longest increasing subsequence problem can be reduced to the edit distance problem. (10%)
參考解答:略
4. Consider the linear-programming system with 9 different constraints $x_1 – x_5 \leq -5, \, x_1 – x_4 \leq -2, \, x_2 – x_1 \leq -3, \, x_2 – x_3 = 8, \, x_3 – x_1 \leq 5, \, x_3 – x_5 \leq 2, \, x_4 – x_3 \leq -3, \, x_5 – x_1 \leq 6, \, x_5 – x_4 \leq 1,$ (1) Draw the constraint graph for these constraints. (2) Solve for the unknowns $x_1, \, x_2, \, x_3, \, x_4,$ and $x_5$ or explain if no solution exists. (10%)
參考解答:略
試題(pdf):連結
有任何問題,或想要完整解釋的,歡迎在下方留言唷!





yuzhi
你好想請問演算法第二題的時間複雜度怎麼算
感謝
mt
總共k個runs所以有k個樹葉,所以每次取出一個record要花O(logk)的時間更新,又因為有n個records,可得總時間為O(nlogk)。
yuzhi
不好意思是演算法部分的第二題 求tight asymptotic upper bound的那道題目
T(n) = 16T(n/2)+Θ(1)這題
mt
這題可以用這棵recursion tree來解釋:
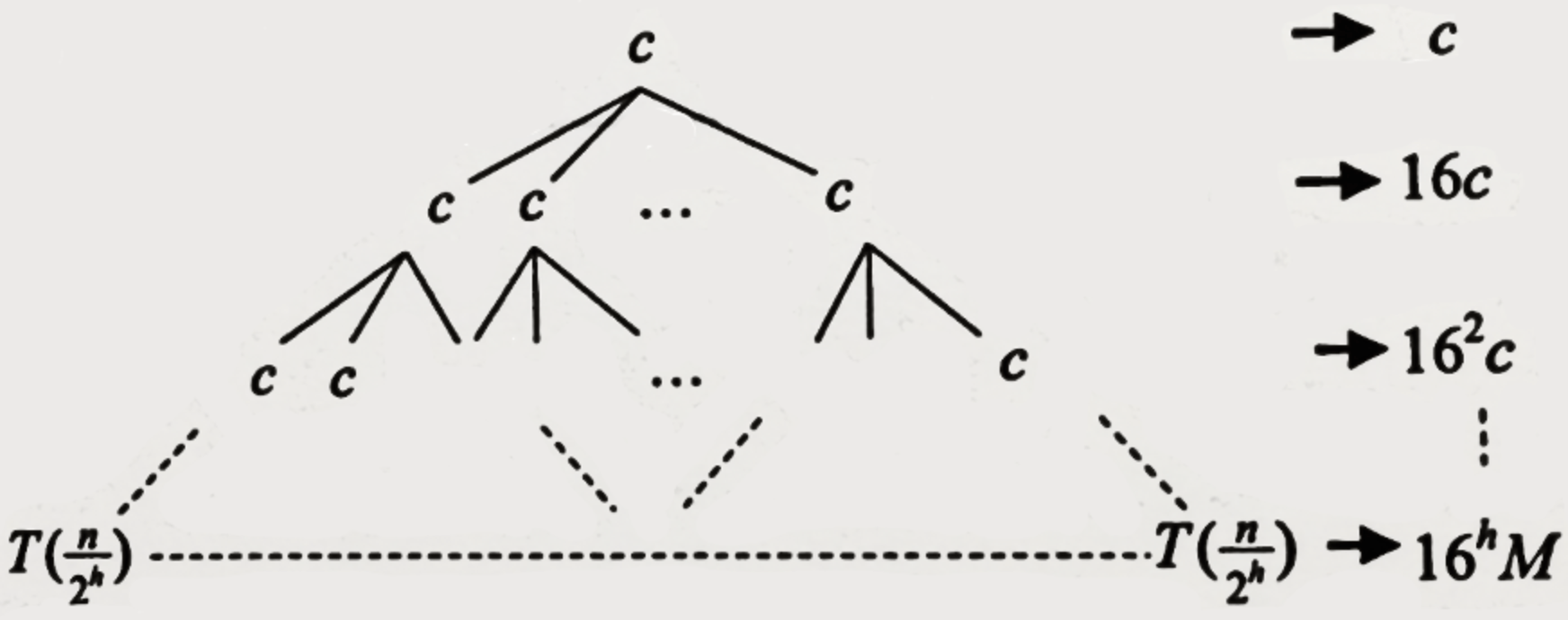
其中h滿足$\dfrac{n}{2^h}^2 \leq M \iff \dfrac{n}{2^h} \leq \sqrt{M} \iff h = \lceil lg(\dfrac{n}{\sqrt{m}}) \rceil$
可得$T(n) = c + 16c + 16^2c + … + 16^{h-1}c + 16^hM = \Theta(16^hM) = \Theta(M \cdot 16^{lg(\dfrac{n}{\sqrt{m}})})$
$= \Theta(M(\dfrac{n}{\sqrt{M}})^4) = \Theta(\dfrac{n^4}{M})$
John
你好,想請問演算法是非題第(2)(3)小題該怎麼改成正確答案?感謝
mt
(2)如果是skew-tree的話要$O(n)$,
(3)的話merge花的時間是$O(n+n+n)=O(n)$。