108成大資聯程設[參考解答]

一、Data Structures (50%)

1. Answer True or False for the following statements. Give correct answer or explain clearly for False statements. (12%)

(1) Let G be a graph with $e$ edges and $v$ vertices. If $G$ is represented by adjacency matrix, DFS requires $O(e^2)$ time.
(2) The path from vertex $u$ to vertex $v$ on a minimal cost spanning tree of an undirected graph $G$ is also a shortest path from $u$ to $v.$
(3) In static hashing, the worst-case number of comparisons needed for a successful search is $O(n)$ for open addressing. The number could be reduced to $O(logn)$ by using chaining method.

參考解答：(1) F (2) F (3) F

---

2. Consider the following AOE network: (18%)

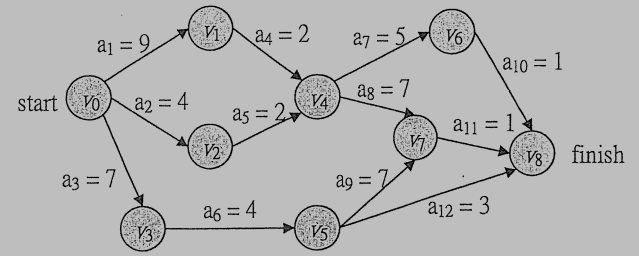
(1) Obtain $e(i)$ and $l(i)$ for all activity $i.$
(2) List all critical activities.
(3) List all critical paths.

參考解答：
(1)

(2) $a_1,a_3,a_4,a_6,a_8,a_9,a_{11}.$
(3) $v_0 \to v_1 \to v_4 \to v_7 \to v_8 \ v_0 \to v_3 \to v_5 \to v_7 \to v_8$

---

3. Given the following 8 runs: (20%)

(1) Draw the corresponding winner tree.
(2) Draw the restructured winner tree after one record has been output.
(3) Draw the loser tree based on the answer of question (2).
(4) Derive the total required time to merge $n$ records through a winner tree with $k$ runs.

參考解答：
(1)

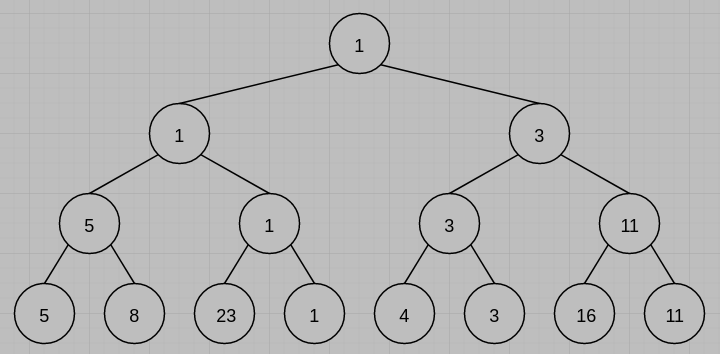
(2)

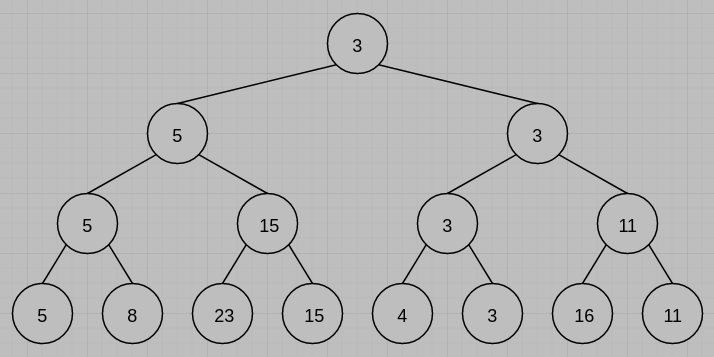
(3)

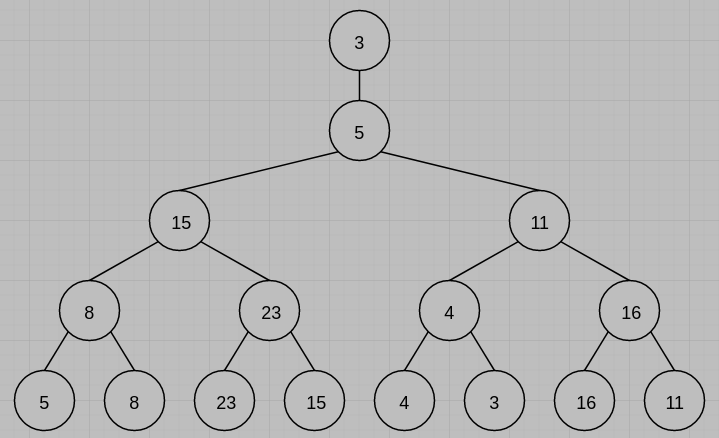
(4) $\Theta(nlgk)$

---

二、Algorithms (50%)

1. (10%) How can we prove the given problem in NP-complete?

參考解答：
(1) Verify that the problem has a non-deterministic algorithm in polynomial time.
(2) Reduce a known NPC problem to the given problem.

---

2. (10%) Give an algorithm that determines whether or not a given undirected graph $G=(V,E)$ contains a cycle. Your algorithm should run in $O(V)$ time, independent of $|E|.$

參考解答：
(1) Input $G(V,E),$ 令 $S$ 為 source.
(2) If $|E| \geq |V|,$ 則 return “cycle found”.
(3) Else enqueue(S), declare empty set $S = \{\}.$
(4) Dequeue(S), $\forall u \in adjList(v)$ 若 $u \in S,$ 則 return “cycle found”, else $S = S \cup \{v\}.$

---

3. (10%) True or false, please explain your answer.

(a) 0-1 knapsack problem can be solved by greedy strategy.
(b) In an undirected graph, we can apply the Depth-First-Search algorithm (DFS) to get tree edges and cross edges.
(c) Based on the top-down approach, we can use the memorization to reduce the time.
(d) Unweighted longest simple path problem has the optimal sub-structure.
(e) If we first apply the topology sort to a directed graph and then run the DFS algorithm on this graph, no back edges can be obtained.

參考解答：(a) F (b) F (c) F (d) F (e) T

---

4. (10%) Use Master theorem to solve the recurrence $T(n) = T(2n/3) + 1.$

參考解答：$\Theta(logn)$

---

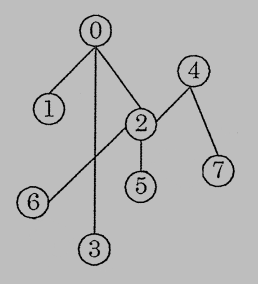
5. (10%) Write the breadth first spanning tree staring at node 0 (visit the smaller number first).

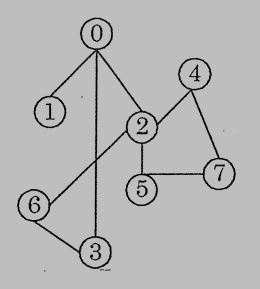
參考解答：

---

試題(pdf)：連結

有任何問題，或想要完整解釋的，歡迎在下方留言唷！