109成大資聯程設[參考解答]

一、Data Structures (50%)

1. Answer True or False for the following statements. Give correct answers for False statements. (30%, 6% for each question)

(1) In static hashing, the worst-case number of comparisons needed for a successful search is $O(n)$ for open addressing. The number could be reduced to $O(logn)$ by using balanced search tree.
(2) Let $d_i$ be the degree of vertex $i$ in a graph $G$ with $|V| = n$ and $|E| = e,$ then $e = \sum_{i = 0}^{n – 1}d_i.$
(3) The path from vertex $u$ to vertex $v$ on a minimal cost spanning tree of an undirected graph $G$ is also a shortest path from $u$ to $v.$
(4) Let $G$ be a graph with $e$ edges and $v$ vertices. If $G$ is represented by adjacency lists, DFS requires $O(ev^2)$ time.
(5) If an AOV network represents a feasible project, its topological order is not unique.

參考解答：(1) T (2) F (3) F (4) F (5) F

---

2. A Bloom Filter consists of $m$ bits of memory and $h$ uniform and independent hash functions $f_1,f_2,…,f_h.$ Each $f_i$ hashes a key $k$ to an integer in the range $[1,m].$ Initially all $m$ filter bits are zero, and the data set is empty. When key $k$ is added to the data set, bits $f_1(k),f_2(k),…,f_h(k)$ of the filter are set to 1. When a query “Is key $k$ in the data set?” is made, bits $f_1(k),f_2(k),…,f_h(k)$ are examined. The query answer is “maybe” if all these bits are 1. Otherwise, the answer is “no.” A filter error occurs whenever the answer is “maybe” and the key is not in the data set. Assume that key $k$ is an integer in the range $[1,n]$ and $u$ updates are made. Compute the probability of filter error for an arbitrary query after the u-th update. (10%)

參考解答：略

---

3. Consider the following graph:

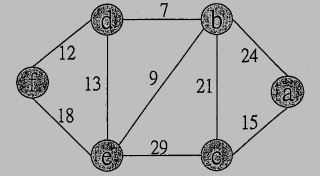
Compute minimum cost and construct minimum spanning tree. (10%)

參考解答：64

---

二、Algorithms (50%)

1. Is $5^{n + 1} = O(5^n)?$ Is $6^{2n} = O(6^n)?$ (10%)

參考解答：Yes, No.

---

2. Give asymptotic upper and lower bound for $T(n) = \sqrt{n}T(\sqrt{n}) + n.$ Assume that $T(n)$ is constant for sufficiently small $n.$ Make your bounds as tight as possible. (10%)

參考解答：$\Theta(nlglgn)$

---

3. Show how the time complexity of quicksort can be made to run in $O(nlgn)$ time. (10%)

參考解答：
(1) Find the median of medians x.
(2) Let x be the pivot key and perform normal quicksort.
$T(n) = 2T(\dfrac{n}{2}) + O(n) = O(nlgn).$

---

4. Determine an Longest Common Subsequence of $<1,0,0,1,0,1,0,1> \text{ and } <0,1,0,1,1,0,1,1,0>.$ (10%)

參考解答：6

---

5. If possible, use the master method to solve $T(n) = 27T(\dfrac{n}{3}) + \Theta(\dfrac{n^3}{lgn}).$ (10%)

參考解答：$\Theta(n^3lglgn)$

---

試題(pdf)：連結

有任何問題，或想要完整解釋的，歡迎在下方留言唷！